Fréchet Space
المؤلف:
Schaefer, H. H.
المصدر:
Topological Vector Spaces. New York: Macmillan, 1966.
الجزء والصفحة:
...
2-8-2021
2347
Fréchet Space
A Fréchet space is a complete and metrizable space, sometimes also with the restriction that the space be locally convex. The topology of a Fréchet space is defined by a countable family of seminorms. For example, the space of smooth functions on ![[0,1]](https://mathworld.wolfram.com/images/equations/FrechetSpace/Inline1.gif)
is a Fréchet space. Its topology is the C-infty topology, which is given by the countable family of seminorms,
Because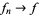 
in this topology implies that 
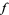is smooth, i.e.,
any Cauchy sequence has a limit in the space of smooth functions, i.e., it is a complete vector space.
REFERENCES:
Schaefer, H. H. Topological Vector Spaces. New York: Macmillan, 1966.
الاكثر قراءة في التبلوجيا
اخر الاخبار
اخبار العتبة العباسية المقدسة
