Species
المؤلف:
Bergeron, F.; Labelle, G.; and Leroux, P.
المصدر:
Combinatorial Species and Tree-Like Structures. Cambridge, England: Cambridge University Press
الجزء والصفحة:
p. 5,
29-7-2021
1325
Species
A species of structures is a rule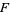 
which
1. Produces, for each finite set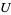 
, a finite set ![F[U]](https://mathworld.wolfram.com/images/equations/Species/Inline3.gif)
,
2. Produces, for each bijection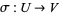 
, a function
![F[sigma]:F[U]->F[V].](https://mathworld.wolfram.com/images/equations/Species/NumberedEquation1.gif) |
(1)
|
The functions ![F[sigma]](https://mathworld.wolfram.com/images/equations/Species/Inline5.gif)
should further satisfy the following functorial properties:
1. For all bijections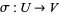 
and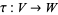 
,
![F[tau degreessigma]=F[tau] degreesF[sigma],](https://mathworld.wolfram.com/images/equations/Species/NumberedEquation2.gif) |
(2)
|
2. For the identity map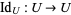 
,
![F[Id_(U)]=Id_(F[U]).](https://mathworld.wolfram.com/images/equations/Species/NumberedEquation3.gif) |
(3)
|
An element ![sigma in F[U]](https://mathworld.wolfram.com/images/equations/Species/Inline9.gif)
is called an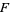 
-structure on 
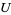(or a structure of species 
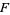on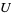 
). The function ![F[sigma]](https://mathworld.wolfram.com/images/equations/Species/Inline14.gif)
is called the transport of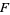 
-structures along 
.
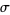REFERENCES:
Bergeron, F.; Labelle, G.; and Leroux, P. Combinatorial Species and Tree-Like Structures. Cambridge, England: Cambridge University Press, p. 5, 1998.
الاكثر قراءة في التبلوجيا
اخر الاخبار
اخبار العتبة العباسية المقدسة
