Open Set
المؤلف:
Croft, H. T.; Falconer, K. J.; and Guy, R. K
المصدر:
Unsolved Problems in Geometry. New York: Springer-Verlag
الجزء والصفحة:
...
25-7-2021
2308
Open Set
Let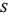 
be a subset of a metric space. Then the set 
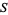is open if every point in 
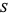has a neighborhood lying in the set. An open set of radius 
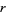and center 
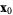is the set of all points 
such that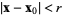 
, and is denoted 
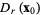. In one-space, the open set is an open interval. In two-space, the open set is a disk. In three-space, the open set is a ball.
More generally, given a topology (consisting of a set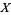 
and a collection of subsets 
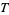), a set is said to be open if it is in 
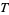. Therefore, while it is not possible for a set to be both finite and open in the topology of the real line (a single point is a closed set), it is possible for a more general topological set to be both finite and open.
The complement of an open set is a closed set. It is possible for a set to be neither open nor closed, e.g., the half-closed interval ![(0,1]](https://mathworld.wolfram.com/images/equations/OpenSet/Inline12.gif)
.
REFERENCES:
Croft, H. T.; Falconer, K. J.; and Guy, R. K. Unsolved Problems in Geometry. New York: Springer-Verlag, p. 2, 1991.
Krantz, S. G. Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 3, 1999.
الاكثر قراءة في التبلوجيا
اخر الاخبار
اخبار العتبة العباسية المقدسة
