Parallel Transport
المؤلف:
Do Carmo, M
المصدر:
Riemannian Geometry. Boston, MA: Birkhäuser, 1993.
الجزء والصفحة:
...
10-7-2021
1476
Parallel Transport
The notion of parallel transport on a manifold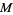 
makes precise the idea of translating a vector field 
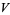along a differentiable curve to attain a new vector field 
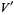which is parallel to 
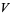. More precisely, let 
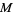be a smooth manifold with affine connectionVector Bundle Connection 
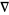, let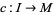 
be a differentiable curve from an interval 
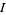into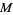 
, and let 
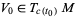be a vector tangent to 
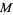at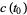 
for some 
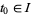. A vector field 
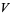is said to be the parallel transport of 
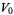along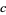 
provided that 
, 
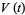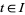, is a vector field for which 
.
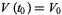Note that the use of the quantifier parallel in the above definition makes reference to the fact that a parallel transport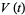 
of a vector field 
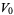along a curve 
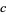is necessarily covariantly constant, i.e., 
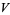satisfies
 |
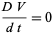(1)
|
for all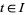 
where, here, 
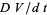denotes the unique covariant derivative of 
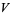associated to 
.
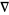A standard result in differential geometry is that, under the above hypotheses, parallel transports are unique.
In addition to the above definition, some literature defines parallel transport in a more function analytic way. Indeed, given an interval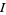 
and a point 
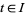, a parallel transport 
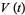of 
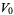along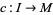 
is nothing more than a linear transformation
 |
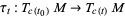(2)
|
which maps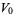 
to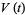 
. It is obvious that this transformation is invertible, its inverse being given simply by parallel transport along the reversed portion of 
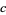from 
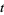to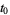 
. The expression 
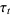has added benefit, too, because despite being defined intrinsically in terms of the affine connecti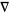on 
on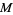 
, it also provides a mechanism whereby one can recover a manifold's affine connection given a collection 
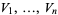of parallel vector fields along a curve 
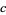. In particular, if 
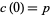and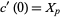 
, then
 |
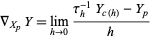(3)
|
where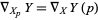 
is the desired vector field given by the connection 
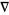and where 
.
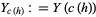REFERENCES:
Do Carmo, M. Riemannian Geometry. Boston, MA: Birkhäuser, 1993.
Spivak, M. A Comprehensive Introduction to Differential Geometry, Vol. 2, 3rd ed. Berkeley, CA: Publish or Perish Press, 1999.
الاكثر قراءة في التبلوجيا
اخر الاخبار
اخبار العتبة العباسية المقدسة
