Given a compact manifold 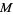 and a transversely orientable codimension-one foliati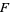on  on 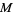 which is tangent to 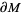, the pair  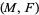is called a generalized Reeb component if the holonomy groups of all leaves in the interior  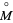are trivial and if all leaves of  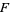are proper. Generalized Reeb components are obvious generalizations of Reeb components.

The introduction of the generalized version of the Reeb component facilitates the proof of many significant results in the theory of 3-manifolds and of foliations. It is well-known that generalized Reeb components are transversely orientable and that a manifold 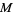 admitting a generalized Reeb component also admits a nice vector field  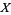(Imanishi and Yagi 1976). Moreover, given a generalized Reeb component 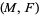,  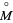is a fibration over .

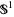Like many notions in geometric topology, the generalized Reeb component can be presented in various contexts. One source describes a generalized Reeb component on a closed 3-manifold 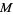 with foliation  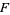to be a submanifold  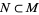of maximal dimension which is bounded by tori {T_alpha}" src="https://mathworld.wolfram.com/images/equations/GeneralizedReebComponent/Inline16.gif" style="height:15px; width:25px" /> such that the orientation of these tori as leaves of 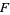 is the same as (or simultaneously opposite to) their orientation as the boundary components of  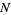(Eliashberg and Thurston 1998). Framed in this way, generalized Reeb components are shown to have deep connections to various notions in foliation theory, e.g., in presenting an existence criterion for a closed 3-manifold  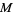to admit a taut foliation.

REFERENCES:

Eliashberg, Y. M. and Thurston, W. P. Confoliations. Providence, RI: Amer. Math. Soc., 1998.

Goodman, S. "Closed Leaves in Foliations of Codimension One." Comm. Math. Helv. 50, 383-388, 1975.

Imanishi, H. and Yagi, K. "On Reeb Components." J. Math. Kyoto Univ. 16, 313-324, 1976.

اخر الاخبار

اخبار العتبة العباسية المقدسة

عباس.. طفل فقد والده فوجد في خدمة زائري عاشوراء وطنًا آمنًا

شعبة الخطابة النسوية تواصل إقامة مجالس العزاء في شهر المحرم الحرام

لليوم الخامس.. العتبة العباسية المقدسة تقيم مجلس عزاء في صحن مرقد أبي الفضل العباس (عليه السلام)

قسم الشؤون الفكرية يقيم مجلس عزاء حسيني في العاصمة التنزانية دار السلام

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد