
Gerbe
 المؤلف:
Brylinski, J
المؤلف:
Brylinski, J
 المصدر:
Loop Spaces, Characteristic Classes and Geometric Quantization. Boston, MA: Birkhäuser, 1993.
المصدر:
Loop Spaces, Characteristic Classes and Geometric Quantization. Boston, MA: Birkhäuser, 1993.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 11-5-2021
11-5-2021
 2145
2145
Gerbe
There are no fewer than two closely related but somewhat different notions of gerbe in mathematics.
For a fixed topological space 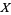 , a gerbe on
, a gerbe on 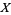 can refer to a stack of groupoids
can refer to a stack of groupoids 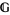 on
on 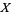 satisfying the properties
satisfying the properties
1. ![X= union <span style=]() {U:G(U)!=emptyset}" src="https://mathworld.wolfram.com/images/equations/Gerbe/Inline5.gif" style="height:15px; width:128px" /> for subsets
{U:G(U)!=emptyset}" src="https://mathworld.wolfram.com/images/equations/Gerbe/Inline5.gif" style="height:15px; width:128px" /> for subsets 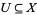 open, and
open, and
2. given objects 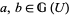 , any point
, any point 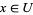 has a neighborhood
has a neighborhood 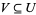 for which there is at least one morphism
for which there is at least one morphism 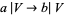 in
in 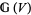 .
.
The second definition is due to Giraud (Brylinski 1993). Given a manifold 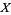 and a Lie group
and a Lie group 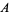 , a gerbe
, a gerbe 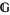 with band
with band 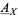 is a sheaf of groupoids over
is a sheaf of groupoids over 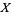 satisfying the following three properties:
satisfying the following three properties:
1. Given any object 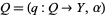 of
of 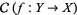 , the sheaf
, the sheaf 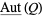 of automorphisms of this object is a sheaf of groups on
of automorphisms of this object is a sheaf of groups on 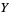 which is locally isomorphic to the sheaf
which is locally isomorphic to the sheaf 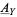 of smooth
of smooth 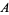 -valued functions. Such a local isomorphism
-valued functions. Such a local isomorphism 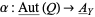 is unique up to inner automorphisms of
is unique up to inner automorphisms of 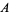 .
.
2. Given two objects 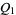 and
and 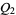 of
of 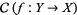 , there exists a surjective local homeomorphism
, there exists a surjective local homeomorphism 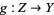 such that
such that 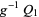 and
and 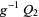 are isomorphic. In particular,
are isomorphic. In particular, 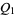 and
and 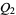 are locally isomorphic.
are locally isomorphic.
3. There exists a surjective local homeomorphism 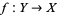 such that the category
such that the category 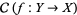 is non-empty.
is non-empty.
Clearly, the notion of a gerbe's band is fundamental for the second definition; though not explicitly mentioned, the band of a gerbe 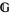 defined by the first definition is also important (Moerdijk 2002). According to Brylinski, gerbes whose bands
defined by the first definition is also important (Moerdijk 2002). According to Brylinski, gerbes whose bands 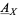 corresponds to a Lie group
corresponds to a Lie group 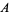 are significant in that they give rise to degree-2 cohomology classes in
are significant in that they give rise to degree-2 cohomology classes in 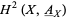 , a fact utilized by Giraud in his study of non-abelian degree-2 cohomology.
, a fact utilized by Giraud in his study of non-abelian degree-2 cohomology.
REFERENCES:
Brylinski, J. Loop Spaces, Characteristic Classes and Geometric Quantization. Boston, MA: Birkhäuser, 1993.
Moerdijk, I. "Introduction to the Language of Stacks and Gerbes." 2002. https://arxiv.org/abs/math/0212266.
 الاكثر قراءة في التبلوجيا
الاكثر قراءة في التبلوجيا
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


