المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Probability Axioms |
 1351
 03:01 مساءً
date: 14-3-2021 |
Author : Doob, J. L. 
Book or Source : "The Development of Rigor in Mathematical Probability (1900-1950)." Amer. Math. Monthly 103 
Page and Part : ...|
Read More
Date: 3-5-2021
1562
Date: 17-4-2021
3529
Date: 27-4-2021
1308
|
Given an event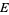 
in a sample space 
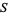which is either finite with 
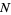elements or countably infinite with 
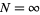elements, then we can write
 |
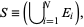and a quantity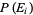 
, called the probability of event 
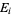, is defined such that
1. 
.
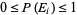2. 
.
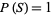3. Additivity: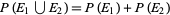 
, where 
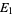and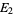 
are mutually exclusive.
4. Countable additivity: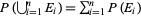 
for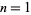 
, 2, ..., 
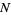where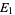 
, 
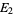, ... are mutually exclusive (i.e., 
).
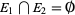REFERENCES:
Doob, J. L. "The Development of Rigor in Mathematical Probability (1900-1950)." Amer. Math. Monthly 103, 586-595, 1996.
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 26-28, 1984.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
