
Tangential Distance, Velocity and Acceleration
 المؤلف:
E. R. Huggins
المؤلف:
E. R. Huggins
 المصدر:
Physics 2000
المصدر:
Physics 2000
 الجزء والصفحة:
337
الجزء والصفحة:
337
 29-11-2020
29-11-2020
 2697
2697
Tangential Distance, Velocity and Acceleration
So far we have used the model of a rotating shaft to illustrate the concepts of angular distance, velocity and acceleration. We now wish to shift the focus of our discussion to the dynamics of a particle traveling along a circular path. For this we will use the model of a small mass m on the end of a massless stick of length r shown in Figure (1). The other end of the stick is attached to and is free to rotate about a fixed axis at the origin of our coordinate system. The presence of the stick ensures that the mass m travels only along a circular path of radius r. The quantity θ( t ) is the angular distance travelled and ω( t ) the angular velocity of the particle.
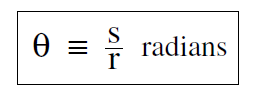 .......(i)
.......(i)
When we are discussing the motion of a particle in a circular orbit, we often want to know how far the particle has travelled, or how fast it is moving. The distance s along the path (we could call the tangential distance) travelled is given by Equation (i) as
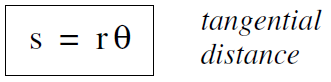 ........(1)
........(1)
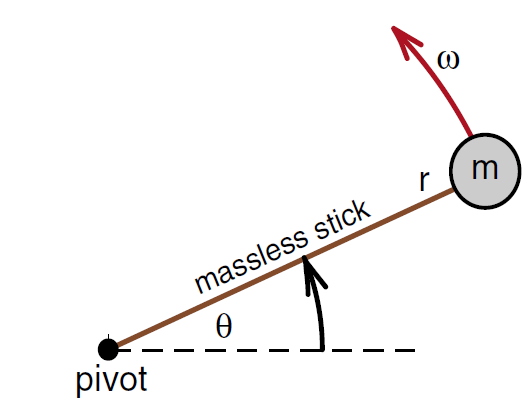
Figure 1: Mass rotating on the end of a massless stick.
The speed of the particle along the path, which we can call the tangential speed vt, is the time derivative of the tangential distance s(t)
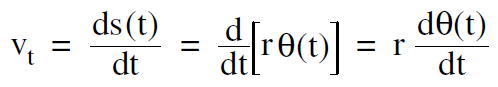
where r comes outside the derivative since it is constant. Since dθ (t) /dt is the angular velocity ω, we get
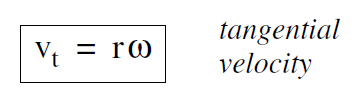
The tangential acceleration at , the acceleration of the particle along its path, is the time derivative of the tangential velocity
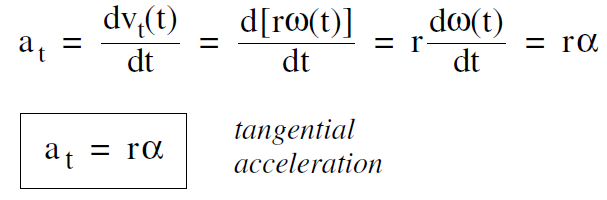
where again we took the constant r outside the derivative, and used α = dω/dt .
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


