Limiting magnitude
 

The amount of energy collected by any aperture is proportional to its area and, therefore, to the square of its diameter. In the case of the eye, the sensitive area responds to the energy which is accepted by the pupil and, accordingly, there is a limit to the strength of radiation that can be detected. For starlight, the limit of unaided eye detection is set at about sixth magnitude. By using a telescope, with its greatly increased aperture over the pupil of the eye, it should be possible to record stars which are much fainter than sixth magnitude.
The brightness of the sixth magnitude star corresponds to the arrival of a certain amount of energy per unit area per unit time. Thus, if the star of naked eye brightness Be is viewed by a telescope, its apparent brightness, Bt , will be given by
(1)
where D and d are the diameters of the telescope and eye pupil respectively, provided that the telescope is used with a sufficient magnification so that all the collected light enters the eye. If me and mt correspond to the magnitude of a star as seen by the naked eye and by the telescope, respectively, the apparent difference in magnitude can be obtained by using Pogson’s equation . Thus,

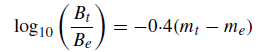
and, by using equation (17.11), this becomes

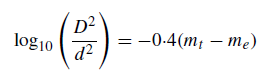
which may be re-written as
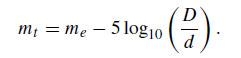(2)

By letting mt correspond to the faintest star that can be detected by the telescope–eye combination (i.e. mt = 6), then the value obtained for me via equation (2), corresponds to the original magnitude of the star. This value is known as the limiting magnitude, mlim, of the telescope and, if a typical value of d = 8·0 mm is used, it can be expressed as
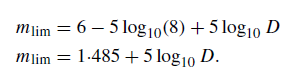(3)
Thus, for a telescope of 500 mm, the theoretical limiting magnitude is approximately 15·0. In this discussion it has been assumed that the transmission efficiency of the telescope is perfect. A typical figure for the efficiency is about 0·65 (including losses in the eyepiece) and, to allow for this, equation (1) should be corrected so that it becomes

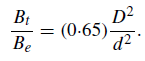
Consequently, equation (2) should be corrected to

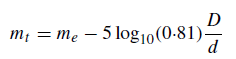
and, by rounding off the figures, the equation expressing the limiting magnitude of the telescope may be written as
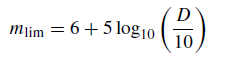(4)
where D is expressed in mm. Thus, in practice, the limiting magnitude for a 500 mm telescope is likely to be about 14·5. Half a magnitude has been ‘lost’ due to the telescope’s imperfect transmission. Equation (4) is again not a hard and fast law, however, as each telescope must be treated individually and also the limiting magnitude will depend on the observer to some extent.

اخر الاخبار

اخبار العتبة العباسية المقدسة

بمشاركة الأمين العام للعتبة العبّاسية المقدّسة.. موكب عزاء السادة الخَدَم يحيي ليلة عاشوراء

صحفيّون يشيدون بالتسهيلات الإعلامية التي تقدّمها العتبة العباسية المقدّسة خلال زيارة عاشوراء

أهالي كربلاء ينظّمون مسيرة الشموع الحسينية إحياءً لليلة العاشر من شهر المحرّم

عبر مجلس عزاء.. العتبة العباسية المقدّسة تحيي ليلة اليوم العاشر من المحرّم

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

اختبار الانفجار الهائل

الكوسمولوجيا وأشكال كالابي - ياو

التخمينات الكوسمولوجيا والنظرية النهائية

النموذج القياسي للكوسمولوجيا، أو علم الكون

تأملات في علم الكون

المذنبات

الصعود إلى الفضاء

اختلاف الليل والنهار

تصنيع الصاروخ و اطلاقة

الكويكبات والمذنبات

صورة الحجر الأزتكي (فهم وإدراك الحضارة الآزيتية )

الهالات المجرية