The Rotational Variables
المؤلف:
Professor John W. Norbury
المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
الجزء والصفحة:
p 132
28-12-2016
2552
The Rotational Variables
Previously we denoted translational position in 1-dimension with the symbol x. If a particle is located on the rim of a circle we often use s instead of x to locate its position around the circumference of the circle. Thus s and x are equivalent translational variables
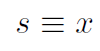
Now the angular position is described by angle which is defined as
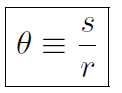
where s (or x) is the translation position and r is the radius of the circle. Notice that angle has no units because s and r both have units of m. The angle defined above is measured in radian, but of course this is not a unit. One complete revolution is 2π radian often also called 360o. (All students should carefully read Pg. 240 of Halliday for a clear distinction between radian and degrees.) Translational position is given by x (or s) and translation displacement was Δx ≡ x2 - x1 (or Δs ≡s2 - s1). Similarly angular displacement is
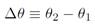
and because 
then it is related to translation displacement by
This is the first entry in the Master Table. Secondly we defined translational average velocity as 
and instantaneous velocity as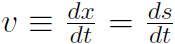 
. Similarly we define average angular velocity as
and instantaneous velocity as
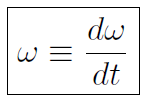
Now because we have 
we must also have 
or 
as relating average velocity and average angular velocity. Similarly
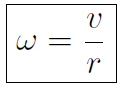
This is the second entry in the Master Table. Finally the angular acceleration α is defined as
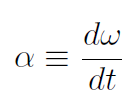
and
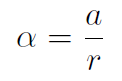
relating angular acceleration α to translational acceleration at. (Notice that a is not the centripetal acceleration. For uniform circular motion α = 0 and at = 0 because the particle moves in a circle at constant speed v and the centripetal acceleration is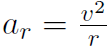 
. For non-uniform circular motion, where the speed keeps increasing (or decreasing) then α ≠ 0 and a ≠ 0).
الاكثر قراءة في الميكانيك
اخر الاخبار
اخبار العتبة العباسية المقدسة
