حركة أي جسيم لا تقتصر بالضرورة على الحركة في خط مستقيم (اعتبر، على سبيل المثال، كرة طائرة أو قمرًا صناعيًا في مدار حول الأرض)، وعموما يتطلب تعيين موضع الجسيم عند زمن t ثلاثة محاور كارتيزية، يرمز لها عادة (t)x، (t)y، (t)z. تقريبا في جميع الحالات التي سوف نناقشها، تكون الحركة محدودة في مستوى، وإذا أخذنا اثنين من محاورنا (مثلا، المحورين x وy) في المستوى. عندئذٍ سيتطلب تحديد الموضع محورين اثنين فقط.

يعمم مباشرة مفهوم السرعة والعجلة على ثلاثة أبعاد إذا كانت إحداثيات الجسيم عند زمن t هي ((t)x، (t)y، (t)z)، وعند t' ((t')x، (t')y، (t')z) هي حينئذ نُعرّف سرعة x المتوسطة خلال الفترة الزمنية 't → t بالمعادلة
 = [x(t')– x(t)]/[t'–t]v_{x ,av} . وتُعرف v_y,av و v_z.av بمعادلتين مماثلتين. كما تُعرَّف سرعة x وسرعة y وسرعة z اللحظية تمامًا كما في حالة الحركة أحادية الأبعاد؛ أي إن:

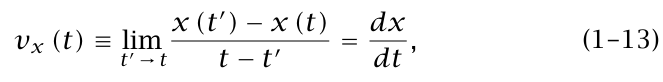
وهكذا. بالمثل، نُعَرِّف  = [x(t')– x(t)]/[t'–t]a_{x ,av} بتعريفات مماثلة لكل من a_y,avg وa_z,avg. وتكون عجلة × اللحظية هي:

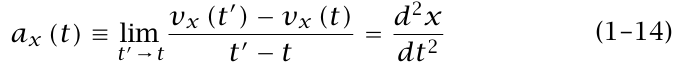
مع تعريفين مماثلين لكل من (a_y(t و(a_z(t

يبدو أن كل ما سبق تعوزه البراعة إلى حَدٍّ ما. ومن البديهي تقريبًا أننا نستطيع استبدال ثلاث معادلات بمعادلة واحدة عن طريق إدخال رمز أكثر أناقة. بل إن هذا الرمز الأكثر أناقة، والذي يُسَمَّى الرمز المُتَجَهِي له ميزة أكثر أهمية: فهو يمكننا من صياغة قوانين الفيزياء بشكل مستقل صراحة عن اتجاه المحاور المحددة التي قمنا باختيارها اعتباطيا. الأقسام التي تُعَرِّف وتشرح الضرب القياسي والضرب الاتجاهي لمتجهين ليست ذات صلة في هذه المرحلة

ومن ثم يمكن حذفها. نقدم الرمز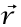 كاختصار للعدد الثلاثي (z ,y ,x) المكون من الإحداثيات الثلاث لجسيم. نسمي 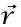متجه الموضع للجسيم ونسمي z وy وx مركبات متجه الموضع بالنسبة إلى مجموعة المحاور المختارة. يُعَبر عادة عن المتجه في النص المطبوع بواسطة حرف سميك (ثقيل) وفي النص المخطوط باليد أو المكتوب بالآلة الكاتبة يُعبر عنه عادة بحرف فوقه سهم أفقي. (بما أن النسخة الأولية من هذا النص كانت مكتوبة على شكل حروف مطبعية؛ فقد رأينا أنه من الأنسب أن يكون الترميز باستخدام السهم.) يُعرف متجها السرعة والعجلة على الصورتين:

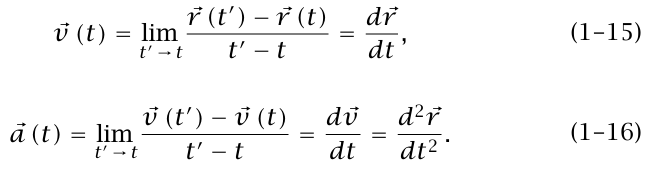
يكون الجسيم متحركا بعجلة تزايدية إذا كان اتجاه متجه السرعة متغيرا، حتى لو ظل مقدار متجه السرعة (مقدار السرعة) ثابتًا.

إحدى المسائل الكينماتيكية المهمة للغاية، والتي حلها لأول مرة نيوتن (عام 1686) هي حساب السرعة اللحظية 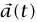 لجسيم متحرك في دائرة بسرعة مقدارها ثابت. نسميها الحركة الدائرية المنتظمة.

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل