دعنا نتأمل جسمًا ماديا (جسيمًا) محدَّد الحركة على طول خط مستقيم معيَّن (مثلًا: سيارة متحركة على طريق سريع مستقيم). إذا اتخذنا نقطةً ما على الخط لتكون نقطة الأصل، فيمكن تعيين موضع الجسيم عند أي لحظة بعدد x يعطي المسافة من نقطة الأصل إلى الجسيم. تُعيَّن قيم x موجبة للنقاط الموجودة على أحد جانبي نقطة الأصل، وتُعيَّن قيم x سالبة للنقاط الموجودة على الجانب الآخر لنقطة الأصل، وبهذا تكون كل قيمة من x مناظرة لنقطة وحيدة. أما أي الاتجاهين هو الموجب وأيهما يكون السالب، فهذا أمر اتفاقي. تعتمد قيمة x العددية بصورة واضحة على وحدة الطول التي نستخدمها (مثلا: القدم، أو المتر، أو الميل). إذا لم يكن الجسيم ساكنا فإن x سوف تتغير مع الزمن.

يُرمز لقيمة x عند زمن t بالرمز (t)x. تُعرَّف السرعة المتوسطة لجسيم خلال الفترة الزمنية من t إلى 't بالعلاقة:

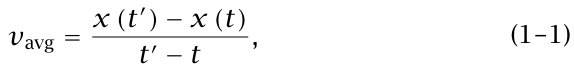
أي إنها التغير في الموضع مقسومًا على التغير في الزمن. إذا رسمنا رسمًا بيانيًّا لـ × مقابل t (مثلا، شكل 1–1) سوف نرى أن [t') – x(t)] / [t' – t)x] ما هو إلا ميل الخط المستقيم المتقطع الذي يصل بين النقطتين اللتين تمثلان موضعي الجسيم عند الزمنين 't وt.

شكل 1–1: مثال للموضع مقابل الزمن.

إن المفهوم الأهم والأكثر دقة هو مفهوم السرعة اللحظية (التي يظهرها عداد السرعة في سيارتك). إذا أبقينا على t ثابتة وتركنا t' تقترب أكثر فأكثر من t، فإن حاصل المقدار [t') – x(t)] / [t' – t)x] سوف يقترب من قيمة نهائية محددة (شريطة أن يكون الرسم البياني لـ × مقابل t سلسًا بدرجة كافية) هي ميل المماس لمنحنى x مقابل t عند النقطة ((t, x(t). يطلق على هذه القيمة النهائية التي يمكن اعتبارها متوسط السرعة خلال فترة زمنية متناهية الصغر تتضمن الزمن t: «السرعة اللحظية عند زمن t»، أو باختصار أكثر «السرعة عند زمن t». وتكتب على الصورة:

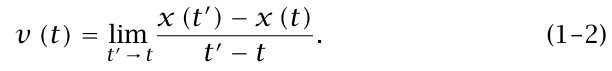
هذه المعادلة مألوفة لأي شخص درس علم حساب التفاضل يسمى الجانب الأيمن «بمشتقة × بالنسبة إلى t» التي كثيرًا ما يُرمز لها بالرمز dx/dt. ومن ثُمَّ يكون

v(t) = dx/dt.

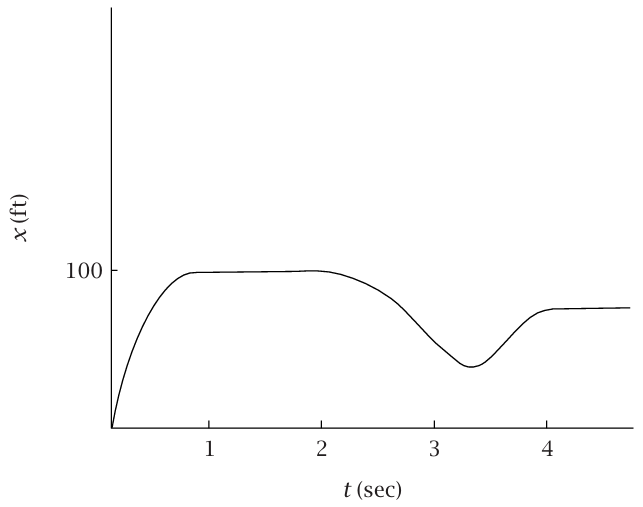
شكل 1–2: مثال آخر على الموضع مقابل الزمن.

إذا كانت (t)x معطاة في هيئة معادلة صريحة، فيمكننا حساب v(t) إما مباشرة من المعادلة (2–1) أو باستخدام قواعد حساب المشتقات التي تُدرس في مناهج حساب التفاضل والتكامل (هذه القواعد، منها مثلا: ^1–d/dt(tⁿ) = ntⁿ، تلخص فقط نتائج تعيين الجانب الأيمن من (2–1) لدوال من (t)x متعددة الصور). أحد التمارين المفيدة هو رسم منحنى بياني كيفي سليم (t)v عندما تكون (t)x معطاة في هيئة منحنى بياني بدلا من أن تكون معطاة في هيئة علاقة رياضياتية. افترض، على سبيل المثال، أن الرسم البياني x (t) هو شكل 1–2 نرسم منحنى بيانيًّا v(t) عن طريق تقدير الميل للمنحنى البياني x مقابل t عند كل نقطة. سنجد أن الميل يكون موجبًا عند 0 = t (وتكون له قيمة عددية تقدر بحوالي 200 قدم / ثانية، مع أننا لسنا مهتمين هنا بالأرقام الدقيقة جدا) ويستمر موجبًا ولكن بقيم متناقصة حتى 1 = t. ويكون الميل صفرًا بين 1 = t و2 = t، ثُمَّ يصبح بعدها سالبًا، وهكذا. إذا كانت قيمة v الموجبة تعني أن الجسم يتحرك إلى الأمام، فإن قيمة v السالبة تعني أن الجسم يتحرك إلى الخلف.) الشكل 1–3 يعرض منحنى بيانيا تقريبيًّا لـ (v(t.

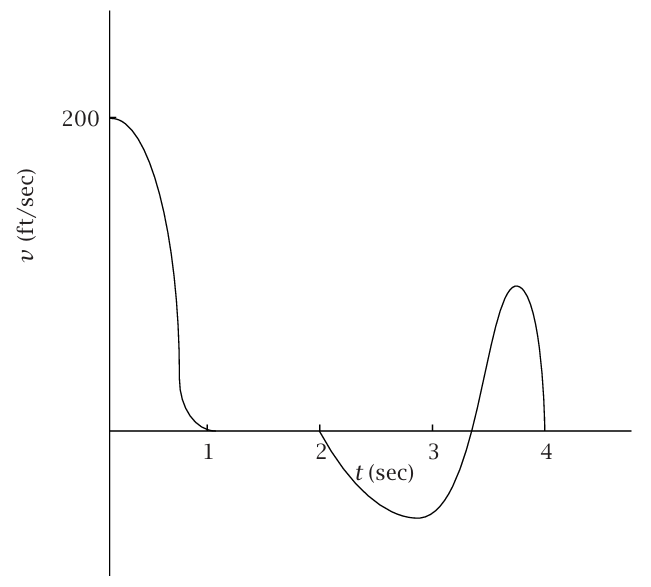
شكل 1–3: المنحنى البياني المناظر للسرعة مقابل الزمن.

إذا كان لدينا (v(t، إما في هيئة علاقة رياضياتية أو منحنى بياني، فإنه يمكننا حساب (t)x. العملية الرياضياتية لإيجاد الدالة (x (t عندما يكون مقدار ميلها (v(t معلومًا عند جميع النقاط تسمى «التكامل». فمثلا، إذا كان 9t³ = v(t) فان x(t) = (9/4) t⁴ + c، حيث ثابت ما (البرهان ببساطة هو حساب dx/dt والتأكد من أننا نحصل على (t)v المرغوبة). ظهور الثابت الاعتباطي c في (t)x ليس مفاجئًا؛ لأن العلم بالسرعة عند جميع الأزمنة ليس كافيًا تمامًا لتعيين الموضع عند جميع الأزمنة على نحو كامل. فينبغي لنا أيضًا أن نعلم من أين بدأ الجسم؛ أي قيمة x عند 0 = t. فإذا كان x(t) = (9/4) t⁴ + c، فإن x(0) = c.

لنفترض أن لدينا مثلا المنحنى البياني (t)v، شكل 1–4. ولنتدبر المستطيل المظلل الذي ارتفاعه (t)v وعرضه Δ، حيث Δ فترة زمنية قصيرة جدًّا.

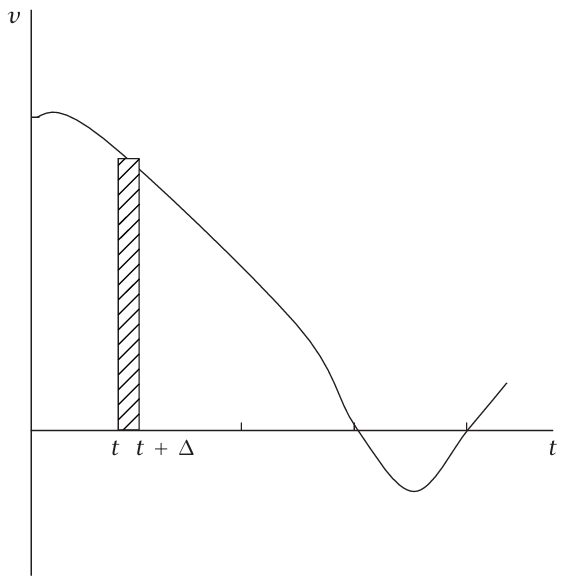
شكل 1–4: المساحة المظللة تمثل الإزاحة خلال Δ + t → t.

مساحة هذا المستطيل هي t) Δ)v، وتساوي الإزاحة (أي التغير في x) للجسيم خلال الفترة الزمنية من t إلى t + Δ. بالمعنى الدقيق، لا تكون العبارة السابقة صحيحة تمامًا إلا إذا كانت (t)v ثابتة خلال الفترة الزمنية من t إلى t + Δ، ولكن إذا كان التغير Δ صغيرا بدرجة كافية فيمكن إهمال تغير v خلال هذه الفترة. إذا كان t₁ وt₂ هما أي زمنين، وقمنا بتقسيم الفترة بينهما إلى فترات كثيرة صغيرة، فإن الإزاحة خلال أي من تلك الفترات الجزئية تساوي تقريبًا مساحة المستطيل المناظر في شكل 1–5. ومن ثم، فإن محصلة الإزاحة (₁t)x – (₂t)x تساوي تقريبًا مجموع مساحات المستطيلات. وكلما كانت الفترات الجزئية أصغر فأصغر، يصير من الممكن إهمال الخطأ في هذا التقريب؛ وبذلك نجد أن المساحة تحت الجزء من منحنى v مقابل t الواقع بين زمن t₁ وt₂ تساوي الإزاحة (₁t)x – (₂t)x التي يجتازها الجسيم خلال تلك الفترة الزمنية.

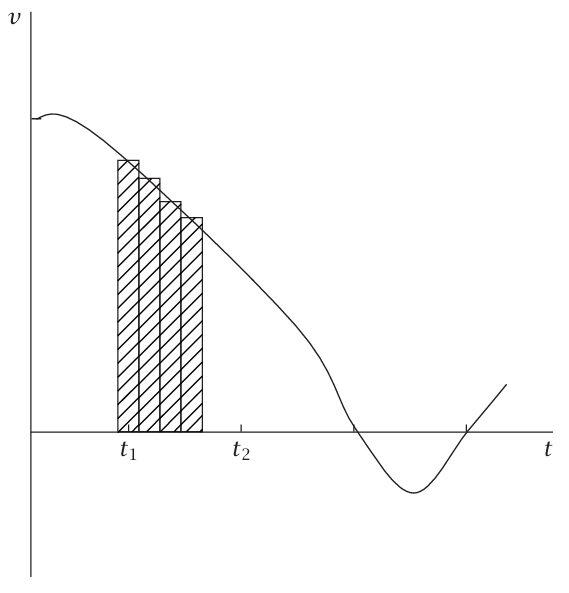
شكل 1–5: المساحة المظللة تمثل الإزاحة خلال t₁ → t₂.

إن العبارة السابقة صحيحة حتى لو أصبحت v سالبة، بشرط أن نُعرّف المساحة بأنها سالبة في المناطق التي تكون فيها ل سالبة بلغة حساب التكامل نكتب:

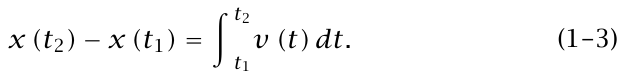
يسمى الجانب الأيمن من المعادلة (3–1) «تكامل (t)v بالنسبة إلى t من t₁ إلى t₂»، ويعرف رياضيًا بأنه نهاية مجموع مساحات المستطيلات في شكل 1–5 عندما تؤول مقادير عرض المستطيلات المفردة إلى صفر.

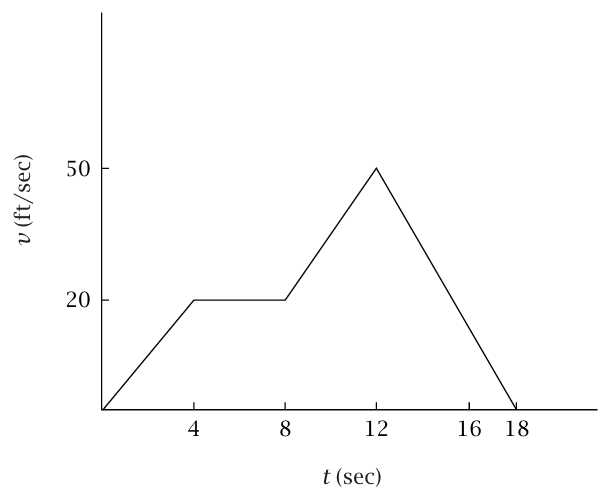
شكل 2–6: رسم بياني للسرعة مقابل الزمن بالنسبة لسيارة.

مثال 1–1 (حساب المسافة والسرعة المتوسطة). يبين شكل 1–6 سرعة سيارة ما كدالة في الزمن. احسب بعد السيارة عن نقطة بدايتها عند sec  6, 12, 16, 18= t. احسب السرعة المتوسطة خلال الفترة من 4 sec  =t  إلى t=15 sec، وخلال الفترة من 0 = t إلى t = 18 sec.

الحل. حساب المساحات '80 = 40 + 40 = (6)x؛ = 140 + 80 + 40 = (12)x

x (18) = 260 + 150 = ;x(16) = 260 + 4(50+ 16.67)/2 = 393.3' 260''

'410. '332.5 = (4)x – (15)x؛ السرعة المتوسطة من 4 = t إلى 15 = t تساوي 30.23 ft/sec ؛ السرعة المتوسطة من 0 = t إلى 18 = t تساوي ft/sec 22.78. ملحوظة بعد أن يتعلم الطلاب المزيد من العلاقات، سوف يستخدم الكثير منهم علاقات رياضياتية بدلًا من الحساب البسيط للمساحات ويحصلون على نتيجة خاطئة.

مثال 1–2. سيدة تقود سيارتها بين كشكين لتحصيل الرسوم يبعدان 60 ميلًا عن بعضهما. تقود الثلاثين ميلا الأولى بسرعة مقدارها 40 ميلا في الساعة. ما مقدار السرعة (الثابتة) التي ينبغي أن تقود بها الأميال المتبقية لكي يكون مقدار سرعتها المتوسطة بين كشكي دفع الرسوم 50 ميلا في الساعة؟

الحل. إذا كان T هو الزمن الكلي مقاسًا بالساعة و50 = 60/T، يكون 1.2 = T. زمن الثلاثين ميلا الأولى هو: 75. = 30/40. وبذلك، يكون زمن الثلاثين ميلا المتبقية هو: 45. = 75. – 1.2. وينبغي أن يكون مقدار السرعة أثناء قطع الثلاثين ميلًا الثانية هو:mph 0.6667 = 45./30.

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل