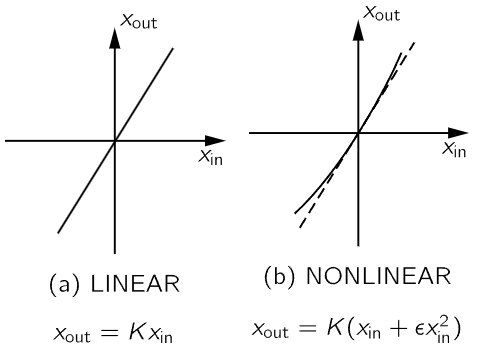
Fig. 50–4. Linear and nonlinear responses.

Finally, in the theory of harmonics there is an important phenomenon which should be remarked upon because of its practical importance—that of nonlinear effects. In all the systems that we have been considering so far, we have supposed that everything was linear, that the responses to forces, say the displacements or the accelerations, were always proportional to the forces. Or that the currents in the circuits were proportional to the voltages, and so on. We now wish to consider cases where there is not a strict proportionality. We think, at the moment, of some device in which the response, which we will call x_out at the time t, is determined by the input x_in at the time t. For example, x_in might be the force and x_out might be the displacement. Or x_in might be the current and x_out the voltage. If the device is linear, we would have

where K is a constant independent of t and of x_in. Suppose, however, that the device is nearly, but not exactly, linear, so that we can write

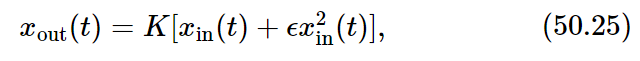
where ϵ is small in comparison with unity. Such linear and nonlinear responses are shown in the graphs of Fig. 50–4.

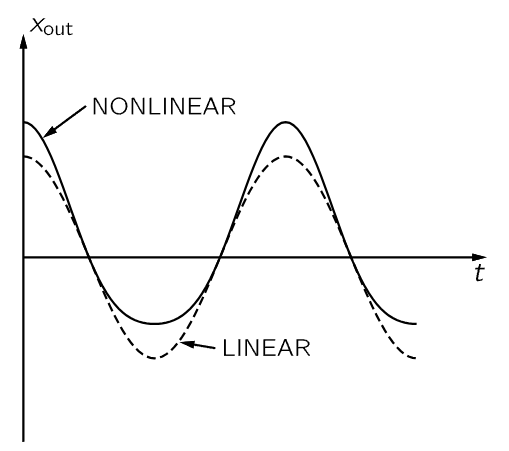
Fig. 50–5. The response of a nonlinear device to the input cos ωt. A linear response is shown for comparison.

Nonlinear responses have several important practical consequences. We shall discuss some of them now. First, we consider what happens if we apply a pure tone at the input. We let x_in=cos ωt. If we plot x_out as a function of time we get the solid curve shown in Fig. 50–5. The dashed curve gives, for comparison, the response of a linear system. We see that the output is no longer a cosine function. It is more peaked at the top and flatter at the bottom. We say that the output is distorted. We know, however, that such a wave is no longer a pure tone, that it will have harmonics. We can find what the harmonics are. Using x_in=cos ωt with Eq. (50.25), we have

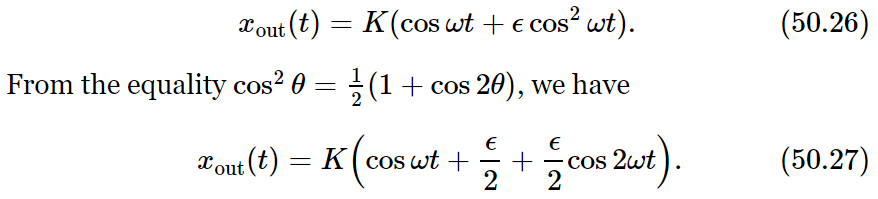
The output has not only a component at the fundamental frequency, that was present at the input, but also has some of its second harmonic. There has also appeared at the output a constant term K(ϵ/2), which corresponds to the shift of the average value, shown in Fig. 50–5. The process of producing a shift of the average value is called rectification.

A nonlinear response will rectify and will produce harmonics of the frequencies at its input. Although the nonlinearity we assumed produced only second harmonics, nonlinearities of higher order—those which have terms like x³_in and x⁴_in, for example—will produce harmonics higher than the second.

Another effect which results from a nonlinear response is modulation. If our input function contains two (or more) pure tones, the output will have not only their harmonics, but still other frequency components. Let x_in=A cosω₁t+B cosω₂t, where now ω₁ and ω₂ are not intended to be in a harmonic relation. In addition to the linear term (which is K times the input) we shall have a component in the output given by

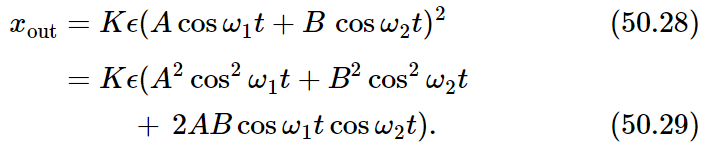
The first two terms in the parentheses of Eq. (50.29) are just those which gave the constant terms and second harmonic terms we found above. The last term is new.

We can look at this new “cross term” AB cosω₁t cosω₂t in two ways. First, if the two frequencies are widely different (for example, if ω₁ is much greater than ω₂) we can consider that the cross term represents a cosine oscillation of varying amplitude. That is, we can think of the factors in this way:

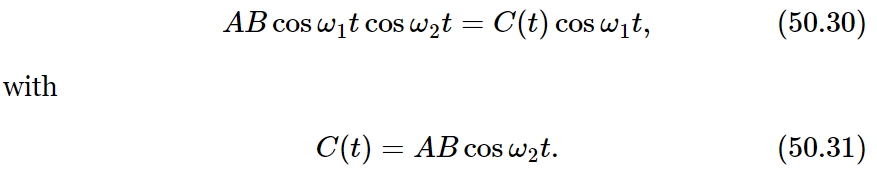
We say that the amplitude of cos ω₁t is modulated with the frequency ω₂.

Alternatively, we can write the cross term in another way:

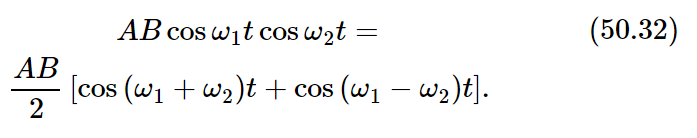
We would now say that two new components have been produced, one at the sum frequency (ω₁+ω₂), another at the difference frequency (ω₁−ω₂).

We have two different, but equivalent, ways of looking at the same result. In the special case that ω₁≫ω₂, we can relate these two different views by remarking that since (ω₁+ω₂) and (ω₁−ω₂) are near to each other we would expect to observe beats between them. But these beats have just the effect of modulating the amplitude of the average frequency ω₁ by one-half the difference frequency 2ω₂. We see, then, why the two descriptions are equivalent.

In summary, we have found that a nonlinear response produces several effects: rectification, generation of harmonics, and modulation, or the generation of components with sum and difference frequencies.

We should notice that all these effects (Eq. 50.29) are proportional not only to the nonlinearity coefficient ϵ, but also to the product of two amplitudes—either A², B², or AB. We expect these effects to be much more important for strong signals than for weak ones.

The effects we have been describing have many practical applications. First, with regard to sound, it is believed that the ear is nonlinear. This is believed to account for the fact that with loud sounds we have the sensation that we hear harmonics and also sum and difference frequencies even if the sound waves contain only pure tones.

The components which are used in sound-reproducing equipment—amplifiers, loudspeakers, etc.—always have some nonlinearity. They produce distortions in the sound—they generate harmonics, etc.—which were not present in the original sound. These new components are heard by the ear and are apparently objectionable. It is for this reason that “Hi-Fi” equipment is designed to be as linear as possible. (Why the nonlinearities of the ear are not “objectionable” in the same way, or how we even know that the nonlinearity is in the loudspeaker rather than in the ear is not clear!)

Nonlinearities are quite necessary, and are, in fact, intentionally made large in certain parts of radio transmitting and receiving equipment. In an am transmitter the “voice” signal (with frequencies of some kilocycles per second) is combined with the “carrier” signal (with a frequency of some megacycles per second) in a nonlinear circuit called a modulator, to produce the modulated oscillation that is transmitted. In the receiver, the components of the received signal are fed to a nonlinear circuit which combines the sum and difference frequencies of the modulated carrier to generate again the voice signal.

When we discussed the transmission of light, we assumed that the induced oscillations of charges were proportional to the electric field of the light—that the response was linear. That is indeed a very good approximation. It is only within the last few years that light sources have been devised (lasers) which produce an intensity of light strong enough so that nonlinear effects can be observed. It is now possible to generate harmonics of light frequencies. When a strong red light passes through a piece of glass, a little bit of blue light—second harmonic—comes out!

مواضيع ذات صلة

The energy theorem

Quality and consonance

The Fourier series

Musical tones

The speed of sound

The propagation of sound

Resonance in nature

Electrical resonance

الرنين الخطر

موسيقى الرياح

عجائب الصدى

هل توجد موجات صوتية في الفضاء؟