In preparation for our second topic, the scattering of light, we must now discuss a certain feature of the phenomenon of interference that we neglected to discuss previously. This is the question of when interference does not occur. If we have two sources S₁ and S₂, with amplitudes A₁ and A₂, and we make an observation in a certain direction in which the phases of arrival of the two signals are ϕ₁ and ϕ₂ (a combination of the actual time of oscillation and the delayed time, depending on the position of observation), then the energy that we receive can be found by compounding the two complex number vectors A₁ and A₂, one at angle ϕ₁ and the other at angle ϕ₂ (as we did in Chapter 29) and we find that the resultant energy is proportional to

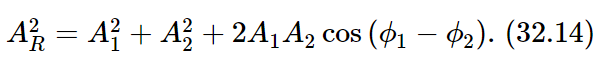
Now if the cross term 2A₁A₂cos(ϕ₁−ϕ₂) were not there, then the total energy that would be received in a given direction would simply be the sum of the energies, A²₁+A²₂, that would be liberated by each source separately, which is what we usually expect. That is, the combined intensity of light shining on something from two sources is the sum of the intensities of the two lights. On the other hand, if we have things set just right and we have a cross term, it is not such a sum, because there is also some interference. If there are circumstances in which this term is of no importance, then we would say the interference is apparently lost. Of course, in nature it is always there, but we may not be able to detect it.

Let us consider some examples. Suppose, first, that the two sources are 7,000,000,000 wavelengths apart, not an impossible arrangement. Then in a given direction it is true that there is a very definite value of these phase differences. But, on the other hand, if we move just a hair in one direction, a few wavelengths, which is no distance at all (our eye already has a hole in it that is so large that we are averaging the effects over a range very wide compared with one wavelength) then we change the relative phase, and the cosine changes very rapidly. If we take the average of the intensity over a little region, then the cosine, which goes plus, minus, plus, minus, as we move around, averages to zero.

So, if we average over regions where the phase varies very rapidly with position, we get no interference.

Another example. Suppose that the two sources are two independent radio oscillators—not a single oscillator being fed by two wires, which guarantees that the phases are kept together, but two independent sources—and that they are not precisely tuned at the same frequency (it is very hard to make them at exactly the same frequency without actually wiring them together). In this case we have what we call two independent sources. Of course, since the frequencies are not exactly equal, although they started in phase, one of them begins to get a little ahead of the other, and pretty soon they are out of phase, and then it gets still further ahead, and pretty soon they are in phase again. So the phase difference between the two is gradually drifting with time, but if our observation is so crude that we cannot see that little time, if we average over a much longer time, then although the intensity swells and falls like what we call “beats” in sound, if these swellings and fallings are too rapid for our equipment to follow, then again this term averages out.

In other words, in any circumstance in which the phase shift averages out, we get no interference!

One finds many books which say that two distinct light sources never interfere. This is not a statement of physics, but is merely a statement of the degree of sensitivity of the technique of the experiments at the time the book was written. What happens in a light source is that first one atom radiates, then another atom radiates, and so forth, and we have just seen that atoms radiate a train of waves only for about 10⁻⁸ sec; after 10⁻⁸ sec, some atom has probably taken over, then another atom takes over, and so on. So, the phases can really only stay the same for about 10⁻⁸ sec. Therefore, if we average for very much more than 10⁻⁸ sec, we do not see an interference from two different sources, because they cannot hold their phases steady for longer than 10⁻⁸ sec. With photocells, very high-speed detection is possible, and one can show that there is an interference which varies with time, up and down, in about 10⁻⁸ sec. But most detection equipment, of course, does not look at such fine time intervals, and thus sees no interference. Certainly, with the eye, which has a tenth-of-a-second averaging time, there is no chance whatever of seeing an interference between two different ordinary sources.

Recently it has become possible to make light sources which get around this effect by making all the atoms emit together in time. The device which does this is a very complicated thing, and has to be understood in a quantum-mechanical way. It is called a laser, and it is possible to produce from a laser a source in which the time during which the phase is kept constant, is very much longer than 10⁻⁸ sec. It can be of the order of a hundredth, a tenth, or even one second, and so, with ordinary photocells, one can pick up the frequency between two different lasers. One can easily detect the pulsing of the beats between two laser sources. Soon, no doubt, someone will be able to demonstrate two sources shining on a wall, in which the beats are so slow that one can see the wall get bright and dark!

Another case in which the interference averages out is that in which, instead of having only two sources, we have many. In this case, we would write the expression for A²_R as the sum of a whole lot of amplitudes, complex numbers, squared, and we would get the square of each one, all added together, plus cross terms between every pair, and if the circumstances are such that the latter average out, then there will be no effects of interference. It may be that the various sources are located in such random positions that, although the phase difference between A₂ and A₃ is also definite, it is very different from that between A₁ and A₂, etc. So, we would get a whole lot of cosines, many plus, many minus, all averaging out.

So it is that in many circumstances we do not see the effects of interference, but see only a collective, total intensity equal to the sum of all the intensities.

مواضيع ذات صلة

The sensation of color

Physiochemistry of color vision

The mechanism of color vision

The chromaticity diagram

Measuring the color sensation

Color depends on intensity

Aberration

The ω,k four-vector

Moving sources

Anomalous refraction

The intensity of reflected light

Optical activity