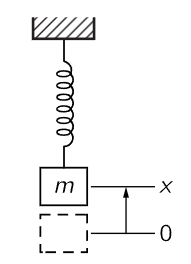
Fig. 21–1. A mass on a spring: a simple example of a harmonic oscillator.

Perhaps the simplest mechanical system whose motion follows a linear differential equation with constant coefficients is a mass on a spring: first the spring stretches to balance the gravity; once it is balanced, we then discuss the vertical displacement of the mass from its equilibrium position (Fig. 21–1). We shall call this upward displacement x, and we shall also suppose that the spring is perfectly linear, in which case the force pulling back when the spring is stretched is precisely proportional to the amount of stretch. That is, the force is −kx (with a minus sign to remind us that it pulls back). Thus the mass times the acceleration must equal −kx:

For simplicity, suppose it happens (or we change our unit of time measurement) that the ratio k/m=1. We shall first study the equation

Later we shall come back to Eq. (21.2) with the k and m explicitly present.

We have already analyzed Eq. (21.3) in detail numerically; when we first introduced the subject of mechanics, we solved this equation (see Eq. 9.12) to find the motion. By numerical integration we found a curve (Fig. 9–4) which showed that if m was initially displaced, but at rest, it would come down and go through zero; we did not then follow it any farther, but of course we know that it just keeps going up and down—it oscillates. When we calculated the motion numerically, we found that it went through the equilibrium point at t=1.570. The length of the whole cycle is four times this long, or t₀=6.28 “sec.” This was found numerically, before we knew much calculus. We assume that in the meantime the Mathematics Department has brought forth a function which, when differentiated twice, is equal to itself with a minus sign. (There are, of course, ways of getting at this function in a direct fashion, but they are more complicated than already knowing what the answer is.) The function is x=cost. If we differentiate this, we find dx/dt=−sin t and d₂x/dt²= −cos t= −x. The function x=cos t starts, at t=0, with x=1, and no initial velocity; that was the situation with which we started when we did our numerical work. Now that we know that x=cos t, we can calculate a precise value for the time at which it should pass x=0. The answer is t=π/2, or 1.57080. We were wrong in the last figure because of the errors of numerical analysis, but it was very close!

Now to go further with the original problem, we restore the time units to real seconds. What is the solution then? First of all, we might think that we can get the constants k and m in by multiplying cost by something. So let us try the equation x=A cos t; then we find dx/dt=−A sin t, and d²x/dt²= −A cos t= −x. Thus, we discover to our horror that we did not succeed in solving Eq. (21.2), but we got Eq. (21.3) again! That fact illustrates one of the most important properties of linear differential equations: if we multiply a solution of the equation by any constant, it is again a solution. The mathematical reason for this is clear. If x is a solution, and we multiply both sides of the equation, say by A, we see that all derivatives are also multiplied by A, and therefore A_x is just as good a solution of the original equation as x was. The physics of it is the following. If we have a weight on a spring, and pull it down twice as far, the force is twice as much, the resulting acceleration is twice as great, the velocity it acquires in a given time is twice as great, the distance covered in a given time is twice as great; but it has to cover twice as great a distance in order to get back to the origin because it is pulled down twice as far. So, it takes the same time to get back to the origin, irrespective of the initial displacement. In other words, with a linear equation, the motion has the same time pattern, no matter how “strong” it is.

That was the wrong thing to do—it only taught us that we can multiply the solution by anything, and it satisfies the same equation, but not a different equation. After a little cut and try to get to an equation with a different constant multiplying x, we find that we must alter the scale of time. In other words, Eq. (21.2) has a solution of the form

(It is important to realize that in the present case, ω₀ is not an angular velocity of a spinning body, but we run out of letters if we are not allowed to use the same letter for more than one thing.) The reason we put a subscript “0” on ω is that we are going to have more omegas before long; let us remember that ω₀ refers to the natural motion of this oscillator. Now we try Eq. (21.4) and this time we are more successful, because dx/dt=−ω₀ sin ω₀t and d²x/dt²= −ω²₀ cos ω₀t= −ω²₀ x. So, at last we have solved the equation that we really wanted to solve. The equation d²x/dt²=−ω²₀x is the same as Eq. (21.2) if ω²₀=k/m.

The next thing we must investigate is the physical significance of ω₀. We know that the cosine function repeats itself when the angle it refers to is 2π. So x=cos ω₀t will repeat its motion, it will go through a complete cycle, when the “angle” changes by 2π. The quantity ω₀t is often called the phase of the motion. In order to change ω₀t by 2π, the time must change by an amount t₀, called the period of one complete oscillation; of course, t₀ must be such that ω₀t₀=2π. That is, ω₀t₀ must account for one cycle of the angle, and then everything will repeat itself—if we increase t by t₀, we add 2π to the phase. Thus

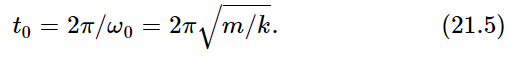
Thus, if we had a heavier mass, it would take longer to oscillate back and forth on a spring. That is because it has more inertia, and so, while the forces are the same, it takes longer to get the mass moving. Or, if the spring is stronger, it will move more quickly, and that is right: the period is less if the spring is stronger.

Note that the period of oscillation of a mass on a spring does not depend in any way on how it has been started, how far down we pull it. The period is determined, but the amplitude of the oscillation is not determined by the equation of motion (21.2). The amplitude is determined, in fact, by how we let go of it, by what we call the initial conditions or starting conditions.

Actually, we have not quite found the most general possible solution of Eq. (21.2). There are other solutions. It should be clear why: because all of the cases covered by x=a cos ω₀t start with an initial displacement and no initial velocity. But it is possible, for instance, for the mass to start at x=0, and we may then give it an impulsive kick, so that it has some speed at t=0. Such a motion is not represented by a cosine—it is represented by a sine. To put it another way, if x=cos ω₀t is a solution, then is it not obvious that if we were to happen to walk into the room at some time (which we would call “t=0”) and saw the mass as it was passing x=0, it would keep on going just the same? Therefore, x=cos ω₀t cannot be the most general solution; it must be possible to shift the beginning of time, so to speak. As an example, we could write the solution this way: x=acosω0(t−t₁), where t₁ is some constant. This also corresponds to shifting the origin of time to some new instant. Furthermore, we may expand

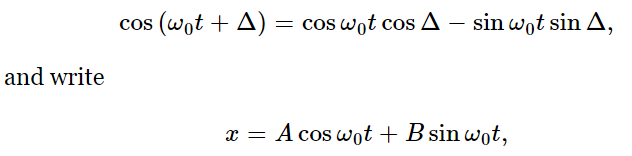
where A=a cos Δ and B=−a sin Δ. Any one of these forms is a possible way to write the complete, general solution of (21.2): that is, every solution of the differential equation d²x/dt²=−ω²₀x that exists in the world can be written as

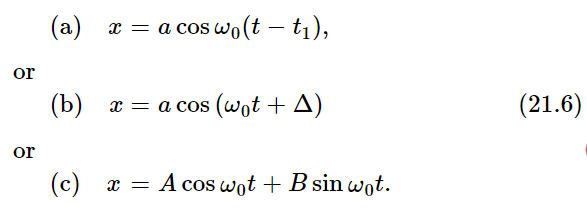
Some of the quantities in (21.6) have names: ω₀ is called the angular frequency; it is the number of radians by which the phase changes in a second. That is determined by the differential equation. The other constants are not determined by the equation, but by how the motion is started. Of these constants, a measures the maximum displacement attained by the mass, and is called the amplitude of oscillation. The constant Δ is sometimes called the phase of the oscillation, but that is a confusion, because other people call ω₀t+Δ the phase, and say the phase changes with time. We might say that Δ is a phase shift from some defined zero. Let us put it differently. Different Δ’s correspond to motions in different phases. That is true, but whether we want to call Δ the phase, or not, is another question.

مواضيع ذات صلة

The Doppler effect

Finding the “apparent” motion

Series and parallel impedances

Analogs in physics

Oscillations in linear systems

Damped oscillations

The energy of an oscillator

The forced oscillator with damping

Complex numbers and harmonic motion

Forced oscillations

Initial conditions for Harmonic motion and circular motion

Harmonic motion and circular motion