
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Friction
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 12
2024-02-11
1533
The foregoing considerations show that a true understanding of Newton’s laws requires a discussion of forces, and it is the purpose of this chapter to introduce such a discussion, as a kind of completion of Newton’s laws. We have already studied the definitions of acceleration and related ideas, but now we have to study the properties of force, and this chapter, unlike the previous chapters, will not be very precise, because forces are quite complicated.
To begin with a particular force, let us consider the drag on an airplane flying through the air. What is the law for that force? (Surely there is a law for every force, we must have a law!) One can hardly think that the law for that force will be simple. Try to imagine what makes a drag on an airplane flying through the air—the air rushing over the wings, the swirling in the back, the changes going on around the fuselage, and many other complications, and you see that there is not going to be a simple law. On the other hand, it is a remarkable fact that the drag force on an airplane is approximately a constant times the square of the velocity, or F≈cv2.
Now what is the status of such a law, is it analogous to F=ma? Not at all, because in the first place this law is an empirical thing that is obtained roughly by tests in a wind tunnel. You say, “Well F=ma might be empirical too.” That is not the reason that there is a difference. The difference is not that it is empirical, but that, as we understand nature, this law is the result of an enormous complexity of events and is not, fundamentally, a simple thing. If we continue to study it more and more, measuring more and more accurately, the law will continue to become more complicated, not less. In other words, as we study this law of the drag on an airplane more and more closely, we find out that it is “falser” and “falser,” and the more deeply we study it, and the more accurately we measure, the more complicated the truth becomes; so in that sense we consider it not to result from a simple, fundamental process, which agrees with our original surmise. For example, if the velocity is extremely low, so low that an ordinary airplane is not flying, as when the airplane is dragged slowly through the air, then the law changes, and the drag friction depends more nearly linearly on the velocity. To take another example, the frictional drag on a ball or a bubble or anything that is moving slowly through a viscous liquid like honey, is proportional to the velocity, but for motion so fast that the fluid swirls around (honey does not but water and air do) then the drag becomes more nearly proportional to the square of the velocity (F=cv2), and if the velocity continues to increase, then even this law begins to fail. People who say, “Well the coefficient changes slightly,” are dodging the issue. Second, there are other great complications: can this force on the airplane be divided or analyzed as a force on the wings, a force on the front, and so on? Indeed, this can be done, if we are concerned about the torques here and there, but then we have to get special laws for the force on the wings, and so on. It is an amazing fact that the force on a wing depends upon the other wing: in other words, if we take the airplane apart and put just one wing in the air, then the force is not the same as if the rest of the plane were there. The reason, of course, is that some of the wind that hits the front goes around to the wings and changes the force on the wings. It seems a miracle that there is such a simple, rough, empirical law that can be used in the design of airplanes, but this law is not in the same class as the basic laws of physics, and further study of it will only make it more and more complicated. A study of how the coefficient c depends on the shape of the front of the airplane is, to put it mildly, frustrating. There just is no simple law for determining the coefficient in terms of the shape of the airplane. In contrast, the law of gravitation is simple, and further study only indicates its greater simplicity.
We have just discussed two cases of friction, resulting from fast movement in air and slow movement in honey. There is another kind of friction, called dry friction or sliding friction, which occurs when one solid body slides on another. In this case a force is needed to maintain motion. This is called a frictional force, and its origin, also, is a very complicated matter. Both surfaces of contact are irregular, on an atomic level. There are many points of contact where the atoms seem to cling together, and then, as the sliding body is pulled along, the atoms snap apart and vibration ensues; something like that has to happen. Formerly the mechanism of this friction was thought to be very simple, that the surfaces were merely full of irregularities and the friction originated in lifting the slider over the bumps; but this cannot be, for there is no loss of energy in that process, whereas power is in fact consumed. The mechanism of power loss is that as the slider snaps over the bumps, the bumps deform and then generate waves and atomic motions and, after a while, heat, in the two bodies. Now it is very remarkable that again, empirically, this friction can be described approximately by a simple law. This law is that the force needed to overcome friction and to drag one object over another depends upon the normal force (i.e., perpendicular to the surface) between the two surfaces that are in contact. Actually, to a fairly good approximation, the frictional force is proportional to this normal force, and has a more or less constant coefficient; that is,

where μ is called the coefficient of friction (Fig. 12–1). Although this coefficient is not exactly constant, the formula is a good empirical rule for judging approximately the amount of force that will be needed in certain practical or engineering circumstances. If the normal force or the speed of motion gets too big, the law fails because of the excessive heat generated. It is important to realize that each of these empirical laws has its limitations, beyond which it does not really work.
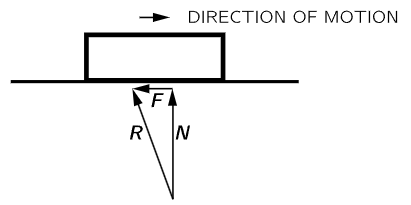
Fig. 12–1. The relation between frictional force and the normal force for sliding contact.
That the formula F=μN is approximately correct can be demonstrated by a simple experiment. We set up a plane, inclined at a small angle θ, and place a block of weight W on the plane. We then tilt the plane at a steeper angle, until the block just begins to slide from its own weight. The component of the weight downward along the plane is W sin θ, and this must equal the frictional force F when the block is sliding uniformly. The component of the weight normal to the plane is W cos θ, and this is the normal force N. With these values, the formula becomes W sin θ=μW cos θ, from which we get μ= sin θ/cos θ= tan θ. If this law were exactly true, an object would start to slide at some definite inclination. If the same block is loaded by putting extra weight on it, then, although W is increased, all the forces in the formula are increased in the same proportion, and W cancels out. If μ stays constant, the loaded block will slide again at the same slope. When the angle θ is determined by trial with the original weight, it is found that with the greater weight the block will slide at about the same angle. This will be true even when one weight is many times as great as the other, and so we conclude that the coefficient of friction is independent of the weight.
In performing this experiment it is noticeable that when the plane is tilted at about the correct angle θ, the block does not slide steadily but in a halting fashion. At one place it may stop, at another it may move with acceleration. This behavior indicates that the coefficient of friction is only roughly a constant, and varies from place to place along the plane. The same erratic behavior is observed whether the block is loaded or not. Such variations are caused by different degrees of smoothness or hardness of the plane, and perhaps dirt, oxides, or other foreign matter. The tables that list purported values of μ for “steel on steel,” “copper on copper,” and the like, are all false, because they ignore the factors mentioned above, which really determine μ. The friction is never due to “copper on copper,” etc., but to the impurities clinging to the copper.
In experiments of the type described above, the friction is nearly independent of the velocity. Many people believe that the friction to be overcome to get something started (static friction) exceeds the force required to keep it sliding (sliding friction), but with dry metals it is very hard to show any difference. The opinion probably arises from experiences where small bits of oil or lubricant are present, or where blocks, for example, are supported by springs or other flexible supports so that they appear to bind.
It is quite difficult to do accurate quantitative experiments in friction, and the laws of friction are still not analyzed very well, in spite of the enormous engineering value of an accurate analysis. Although the law F=μN is fairly accurate once the surfaces are standardized, the reason for this form of the law is not really understood. To show that the coefficient μ is nearly independent of velocity requires some delicate experimentation, because the apparent friction is much reduced if the lower surface vibrates very fast. When the experiment is done at very high speed, care must be taken that the objects do not vibrate relative to one another, since apparent decreases of the friction at high speed are often due to vibrations. At any rate, this friction law is another of those semiempirical laws that are not thoroughly understood, and in view of all the work that has been done it is surprising that more understanding of this phenomenon has not come about. At the present time, in fact, it is impossible even to estimate the coefficient of friction between two substances. It was pointed out above that attempts to measure μ by sliding pure substances such as copper on copper will lead to spurious results, because the surfaces in contact are not pure copper, but are mixtures of oxides and other impurities. If we try to get absolutely pure copper, if we clean and polish the surfaces, outgas the materials in a vacuum, and take every conceivable precaution, we still do not get μ. For if we tilt the apparatus even to a vertical position, the slider will not fall off—the two pieces of copper stick together! The coefficient μ, which is ordinarily less than unity for reasonably hard surfaces, becomes several times unity! The reason for this unexpected behavior is that when the atoms in contact are all of the same kind, there is no way for the atoms to “know” that they are in different pieces of copper. When there are other atoms, in the oxides and greases and more complicated thin surface layers of contaminants in between, the atoms “know” when they are not on the same part. When we consider that it is forces between atoms that hold the copper together as a solid, it should become clear that it is impossible to get the right coefficient of friction for pure metals.
The same phenomenon can be observed in a simple home-made experiment with a flat glass plate and a glass tumbler. If the tumbler is placed on the plate and pulled along with a loop of string, it slides fairly well and one can feel the coefficient of friction; it is a little irregular, but it is a coefficient. If we now wet the glass plate and the bottom of the tumbler and pull again, we find that it binds, and if we look closely, we shall find scratches, because the water is able to lift the grease and the other contaminants off the surface, and then we really have a glass-to-glass contact; this contact is so good that it holds tight and resists separation so much that the glass is torn apart; that is, it makes scratches.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















