Circumpolar stars
المؤلف:
A. Roy, D. Clarke
المصدر:
Astronomy - Principles and Practice 4th ed
الجزء والصفحة:
p 63
24-7-2020
1909
Circumpolar stars
Consider the celestial sphere for an observer in latitude ∅N (figure 1). The parallels of declination of a number of stars have been inserted with arrowheads to show that as time passes their hour angles increase steadily as the celestial sphere rotates.
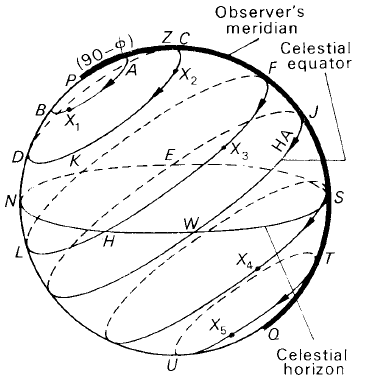
Figure 1. Circumpolar stars.
The stars can be put into three classes:
(a) stars that are above the horizon for all values of their hour angle,
(b) stars that are below the horizon for all values of their hour angle,
(c) stars that are seen to rise and set.
Stars in class (a) are circumpolar stars. Examples of these in figure 1. are stars X1 and X2. Star X1 transits at A north of the zenith in contrast to star X2’s transit which is south of the zenith. These transits are referred to as upper transit or upper culmination. Both stars also transit below the pole; such transits are described as below pole or at lower culmination.
Now CD is the parallel of declination of star X2. In order that the star is circumpolar, then, we must have
PD < PN
that is
90 − δ < ∅.
In order that the upper transit should be south of the zenith we must have
PC > PZ
that is
90 −δ > 90 − ∅
or
∅ > δ.
Stars in class (b) are never seen by the observer. The ancients who introduced the constellations were unaware of such stars, thus explaining why a roughly circular area of the celestial sphere in the vicinity of the south celestial pole is not represented in the ancient constellations. In the diagram, star X4, of declination δ S, is the limiting case. Now
J S = 90 − ∅ SQ = 90 − δ.
Also
J Q = 90◦
Hence, we have
180 − ∅ − δ = 90
or
∅ + δ = 90. (1.1)
Hence, δ = 90 − ∅ is the limiting declination of a star if it is to remain below the horizon. If δ < 90 − ∅, the star comes above the horizon. By putting a value in equation (1.1) for the declination of the stars at the edge of the roughly circular area not represented in the ancient constellations, it is found that the constellation-makers must have lived in a latitude somewhere between 34◦ and 36◦ N.
Most stars are found in class (c), that is they rise and transit, then set. For example, star X3 moves along its parallel of declination (the small circle FHLK), setting at H, rising at K and transiting at F.
الاكثر قراءة في النجوم
اخر الاخبار
اخبار العتبة العباسية المقدسة
