X-ray : Rotating Crystal Method

To describe the periodic, three dimensional nature of crystals, the Laue equations are employed:

where a, b, and c are the three axes of the unit cell, θo, o, ?o are the angles of incident radiation, and ?, ?, ? are the angles of the diffracted radiation. A diffraction signal (constructive interference) will arise when h, k, and l are integer values. The rotating crystal method employs these equations. X-ray radiation is shown onto a crystal as it rotates around one of its unit cell axis. The beam strikes the crystal at a 90 degree angle. Using equation 1 above, we see that if θo is 90 degrees, then cosθo=0. For the equation to hold true, we can set h=0, granted that heta= 90. The above three equations will be satisfied at various points as the crystal rotates. This gives rise to a diffraction pattern (shown in the image below as multiple h values). The cylindrical film is then unwrapped and developed. The following equation can be used to determine the length axis around which the crystal was rotated:

where a is the length of the axis, y is the distance from h=0 to the h of interest, r is the radius of the firm, and ? is the wavelength of the x-ray radiation used. The first length can be determined with ease, but the other two require far more work, including remounting the crystal so that it rotates around that particular axis.

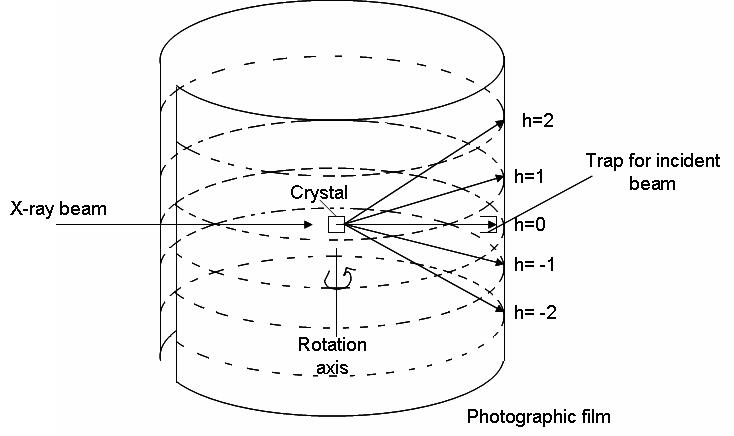
Figure 1:

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد

مواضيع ذات صلة

التحليل الطيفي

الإشعاع الكهرومغناطيسي Electromagnetic Radiation

مكونات الجهاز المستخدم في التحليل الالي

طرق التحليل الآلي Instrumental Methods) )

اطياف الاشعة تحت الحمراء

تشتت الدوران البصري والانكسار المزدوج الدائري

مطياف الفلورة (التألق) Fluorescence spectroscopy

الضوء المستقطب والنشاط الضوئي

الدوران النوعي

البولاريمتر

Electrophoretic Mobility 2

Capillary Electrophoresis 2