
Law of Cosines
 المؤلف:
Abramowitz, M. and Stegun, I. A.
المؤلف:
Abramowitz, M. and Stegun, I. A.
 المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover,
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover,
 الجزء والصفحة:
...
الجزء والصفحة:
...
 12-10-2019
12-10-2019
 2323
2323
Law of Cosines
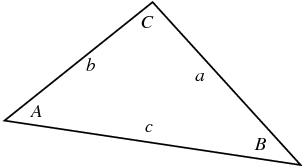
Let 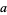 ,
, 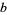 , and
, and 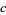 be the lengths of the legs of a triangle opposite angles
be the lengths of the legs of a triangle opposite angles 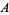 ,
, 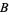 , and
, and 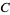 . Then the law of cosines states
. Then the law of cosines states
Solving for the cosines yields the equivalent formulas
This law can be derived in a number of ways. The definition of the dot product incorporates the law of cosines, so that the length of the vector from 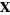 to
to 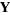 is given by
is given by
where 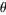 is the angle between
is the angle between 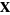 and
and 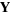 .
.
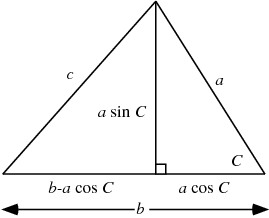
The formula can also be derived using a little geometry and simple algebra. From the above diagram,
The law of cosines for the sides of a spherical triangle states that
(Beyer 1987). The law of cosines for the angles of a spherical triangle states that
(Beyer 1987).
For similar triangles, a generalized law of cosines is given by
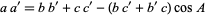 |
(19)
|
(Lee 1997). Furthermore, consider an arbitrary tetrahedron 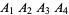 with triangles
with triangles 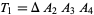 ,
, 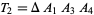 ,
, 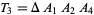 , and
, and 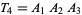 . Let the areas of these triangles be
. Let the areas of these triangles be 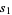 ,
, 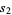 ,
, 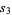 , and
, and 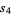 , respectively, and denote the dihedral angle with respect to
, respectively, and denote the dihedral angle with respect to 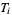 and
and 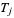 for
for 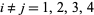 by
by 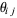 . Then
. Then
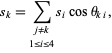 |
(20)
|
which gives the law of cosines in a tetrahedron,
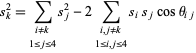 |
(21)
|
(Lee 1997). A corollary gives the nice identity
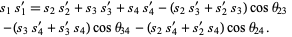 |
(22)
|
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 79, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 148-149, 1987.
Lee, J. R. "The Law of Cosines in a Tetrahedron." J. Korea Soc. Math. Ed. Ser. B: Pure Appl. Math. 4, 1-6, 1997.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


