Weierstrass Sigma Function
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
"Weierstrass Elliptic and Related Functions." Ch. 18 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
23-4-2019
2086
Weierstrass Sigma Function
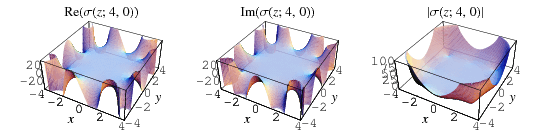
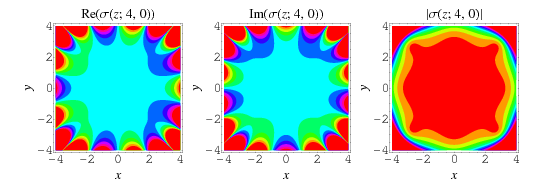
The quasiperiodic function defined by
 |
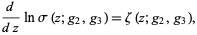(1)
|
where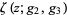 
is the Weierstrass zeta function and
 |
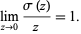(2)
|
(As in the case of other Weierstrass elliptic functions, the invariants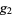 
and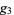 
are frequently suppressed for compactness.) Then
 |
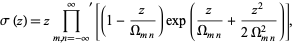(3)
|
where the term with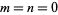 
is omitted from the product and 
.
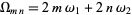Amazingly,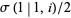 
, where 
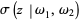is the Weierstrass sigma function with half-periods 
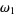and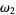 
, has a closed form in terms of 
, 
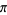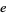, and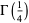 
. This constant is known as the Weierstrass constant.
In addition,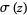 
satisfies
and
 |
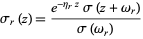(6)
|
for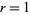 
, 2, 3. The function is implemented in the Wolfram Language as WeierstrassSigma[u, ![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/WeierstrassSigmaFunction/Inline21.gif" style="height:14px; width:5px" />g2, g3![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/WeierstrassSigmaFunction/Inline22.gif" style="height:14px; width:5px" />].
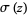can be expressed in terms of Jacobi theta functions using the expression
 |
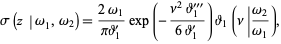(7)
|
where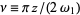 
, and
There is a beautiful series expansion for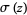 
, given by the double series
 |
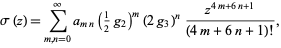(10)
|
where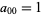 
, 
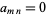for either subscript negative, and other values are gives by the recurrence relation
 |
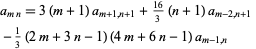(11)
|
(Abramowitz and Stegun 1972, pp. 635-636). The following table gives the values of the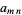 
coefficients for small 
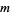and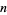 
.
| |
 |
 |
 |
 |
 |
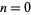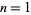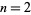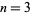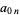1 |
-3 |
-54 |
14904 |
 |
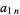-1 |
-18 |
4968 |
502200 |
 |
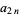-9 |
513 |
257580 |
162100440 |
 |
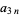69 |
33588 |
20019960 |
-9465715080 |
 |
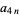321 |
2808945 |
-376375410 |
-4582619446320 |
 |
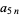160839 |
-41843142 |
-210469286736 |
-1028311276281264 |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Weierstrass Elliptic and Related Functions." Ch. 18 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 627-671, 1972.
Brezhnev, Y. V. "Uniformisation: On the Burnside Curve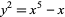 
." 9 Dec 2001. http://arxiv.org/abs/math.CA/0111150.
Knopp, K. "Example: Weierstrass's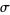 
-Function." §2d in Theory of Functions Parts I and II, Two Volumes Bound as One, Part II.New York: Dover, pp. 27-30, 1996.
Tölke, F. "Spezielle Weierstraßsche Sigma-Funktionen." Ch. 9 in Praktische Funktionenlehre, dritter Band: Jacobische elliptische Funktionen, Legendresche elliptische Normalintegrale und spezielle Weierstraßsche Zeta- und Sigma Funktionen. Berlin: Springer-Verlag, pp. 164-180, 1967.
Whittaker, E. T. and Watson, G. N. "The Function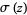 
." §20.42 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 447-448, 450-452, and 458-461, 1990.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
