Clebsch-Gordan Coefficient
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
"Vector-Addition Coefficients." §27.9 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover,
الجزء والصفحة:
...
16-4-2019
3237
Clebsch-Gordan Coefficient
Clebsch-Gordan coefficients are mathematical symbol used to integrate products of three spherical harmonics. Clebsch-Gordan coefficients commonly arise in applications involving the addition of angular momentum in quantum mechanics. If products of more than three spherical harmonics are desired, then a generalization known as Wigner 6j-symbols or Wigner 9j-symbols is used.
The Clebsch-Gordan coefficients are variously written as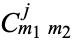 
, 
, 
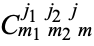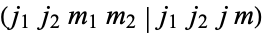, or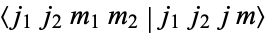 
. The Clebsch-Gordan coefficients are implemented in the Wolfram Language as ClebschGordan[![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline5.gif" style="height:14px; width:5px" />j1, m1![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline6.gif" style="height:14px; width:5px" />, ![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline7.gif" style="height:14px; width:5px" />j2, m2![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline8.gif" style="height:14px; width:5px" />, ![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline9.gif" style="height:14px; width:5px" />j, m![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline10.gif" style="height:14px; width:5px" />].
The Clebsch-Gordan coefficients are defined by
 |
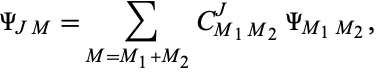(1)
|
where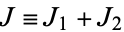 
, and satisfy
 |
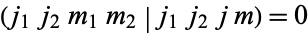(2)
|
for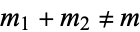 
.
Care is needed in interpreting analytic representations of Clebsch-Gordan coefficients since these coefficients are defined only on measure zero sets. As a result, "generic" symbolic formulas may not hold it certain cases, if at all. For example, ClebschGordan[![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline13.gif" style="height:14px; width:5px" />1, 0![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline14.gif" style="height:14px; width:5px" />, ![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline15.gif" style="height:14px; width:5px" />j2, 0![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline16.gif" style="height:14px; width:5px" />, ![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline17.gif" style="height:14px; width:5px" />2, 0![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline18.gif" style="height:14px; width:5px" />] evaluates to an expression that is "generically" correct but not correct for the special case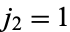 
, whereas ClebschGordan[![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline20.gif" style="height:14px; width:5px" />1, 0![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline21.gif" style="height:14px; width:5px" />, ![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline22.gif" style="height:14px; width:5px" />1, 0![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline23.gif" style="height:14px; width:5px" />, ![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline24.gif" style="height:14px; width:5px" />2, 0![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/Clebsch-GordanCoefficient/Inline25.gif" style="height:14px; width:5px" />] evaluates to the correct value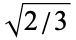 
.
The coefficients are subject to the restrictions that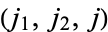 
be positive integers or half-integers, 
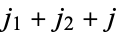is an integer, 
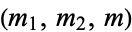are positive or negative integers or half integers,
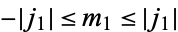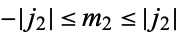and 
, 
, and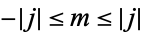 
(Abramowitz and Stegun 1972, p. 1006). In addition, by use of symmetry relations, coefficients may always be put in the standard form 
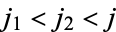and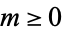 
.
The Clebsch-Gordan coefficients are sometimes expressed using the related Racah V-coefficients,
 |
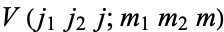(6)
|
or Wigner 3j-symbols. Connections among the three are
 |
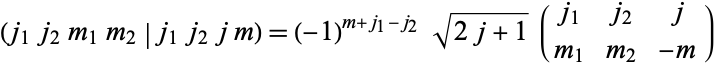(7)
|
 |
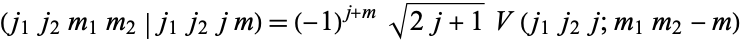(8)
|
 |
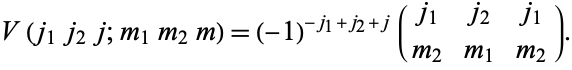(9)
|
They have the symmetry
 |
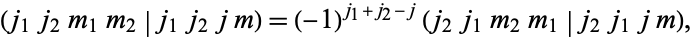(10)
|
and obey the orthogonality relationships
 |
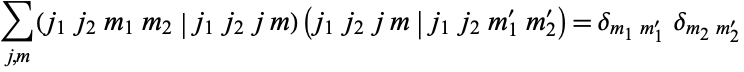(11)
|
 |
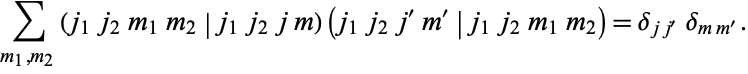(12)
|
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Vector-Addition Coefficients." §27.9 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 1006-1010, 1972.
Cohen-Tannoudji, C.; Diu, B.; and Laloë, F. "Clebsch-Gordan Coefficients." Complement 
in Quantum Mechanics, Vol. 2. New York: Wiley, pp. 1035-1047, 1977.
Condon, E. U. and Shortley, G. §3.6-3.14 in The Theory of Atomic Spectra. Cambridge, England: Cambridge University Press, pp. 56-78, 1951.
Fano, U. and Fano, L. Basic Physics of Atoms and Molecules. New York: Wiley, p. 240, 1959.
Messiah, A. "Clebsch-Gordan (C.-G.) Coefficients and '3j' Symbols." Appendix C.I in Quantum Mechanics, Vol. 2. Amsterdam, Netherlands: North-Holland, pp. 1054-1060, 1962.
Rose, M. E. Elementary Theory of Angular Momentum. New York: Dover, 1995.
Shore, B. W. and Menzel, D. H. "Coupling and Clebsch-Gordan Coefficients." §6.2 in Principles of Atomic Spectra. New York: Wiley, pp. 268-276, 1968.
Sobel'man, I. I. "Angular Momenta." Ch. 4 in Atomic Spectra and Radiative Transitions, 2nd ed. Berlin: Springer-Verlag, 1992.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
