Modified Bessel Function of the First Kind
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
"Modified Bessel Functions I and K." §9.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
25-3-2019
3489
Modified Bessel Function of the First Kind
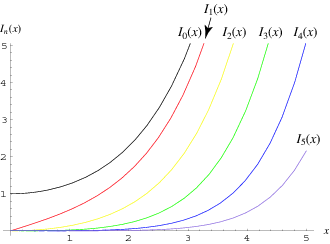
A function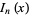 
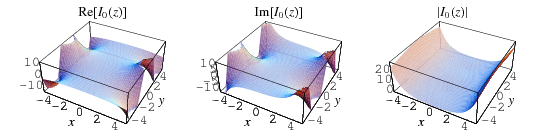
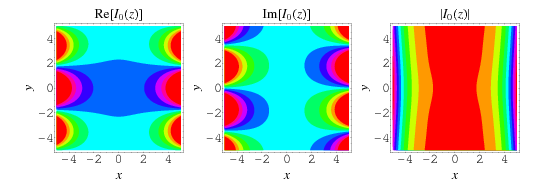
which is one of the solutions to the modified Bessel differential equation and is closely related to the Bessel function of the first kind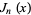 
. The above plot shows 
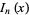for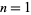 
, 2, ..., 5. The modified Bessel function of the first kind is implemented in the Wolfram Language as BesselI[nu, z].
The modified Bessel function of the first kind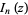 
can be defined by the contour integral
 |
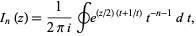(1)
|
where the contour encloses the origin and is traversed in a counterclockwise direction (Arfken 1985, p. 416).
In terms of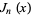 
,
 |
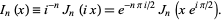(2)
|
For a real number 
, the function can be computed using
 |
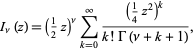(3)
|
where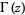 
is the gamma function. An integral formula is
 |
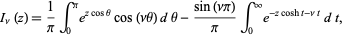(4)
|
which simplifies for 
an integer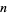 
to
 |
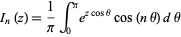(5)
|
(Abramowitz and Stegun 1972, p. 376).
A derivative identity for expressing higher order modified Bessel functions in terms of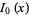 
is
 |
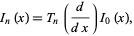(6)
|
where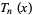 
is a Chebyshev polynomial of the first kind.
The special case of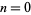 
gives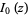 
as the series
 |
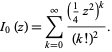(7)
|
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Modified Bessel Functions 
and 
." §9.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 374-377, 1972.
Arfken, G. "Modified Bessel Functions,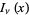 
and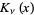 
." §11.5 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 610-616, 1985.
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Bessel Functions of Fractional Order, Airy Functions, Spherical Bessel Functions." §6.7 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 234-245, 1992.
Spanier, J. and Oldham, K. B. "The Hyperbolic Bessel Functions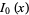 
and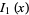 
" and "The General Hyperbolic Bessel Function 
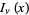." Chs. 49-50 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 479-487 and 489-497, 1987.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
