A complex function is said to be analytic on a region 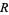 if it is complex differentiable at every point in 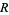. The terms holomorphic function, differentiable function, and complex differentiable function are sometimes used interchangeably with "analytic function" (Krantz 1999, p. 16). Many mathematicians prefer the term "holomorphic function" (or "holomorphic map") to "analytic function" (Krantz 1999, p. 16), while "analytic" appears to be in widespread use among physicists, engineers, and in some older texts (e.g., Morse and Feshbach 1953, pp. 356-374; Knopp 1996, pp. 83-111; Whittaker and Watson 1990, p. 83).

If a complex function is analytic on a region 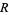, it is infinitely differentiable in 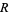. A complex function may fail to be analytic at one or more points through the presence of singularities, or along lines or line segments through the presence of branch cuts.

A complex function that is analytic at all finite points of the complex plane is said to be entire. A single-valued function that is analytic in all but possibly a discrete subset of its domain, and at those singularities goes to infinity like a polynomial (i.e., these exceptional points must be poles and not essential singularities), is called a meromorphic function.

REFERENCES:

Knopp, K. "Analytic Continuation and Complete Definition of Analytic Functions." Ch. 8 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part I. New York: Dover, pp. 83-111, 1996.

Krantz, S. G. "Alternative Terminology for Holomorphic Functions." §1.3.6 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 16, 1999.

Morse, P. M. and Feshbach, H. "Analytic Functions." §4.2 in Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 356-374, 1953.

Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.