Min Max

Min   Max       Re       Im

The exponential function is the entire function defined by

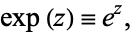(1)

where e is the solution of the equation 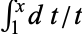 so that 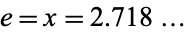.  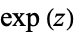is also the unique solution of the equation  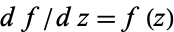with .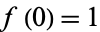

The exponential function is implemented in the Wolfram Language as Exp[z].

It satisfies the identity

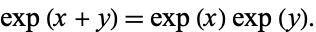(2)

If ,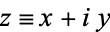

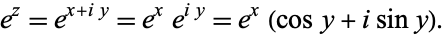(3)

The exponential function satisfies the identities

			(4)
			(5)
			(6)
			(7)

where 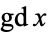 is the Gudermannian (Beyer 1987, p. 164; Zwillinger 1995, p. 485).

The exponential function has Maclaurin series

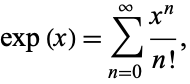(8)

and satisfies the limit

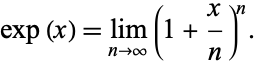(9)

If

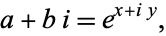(10)

then

			(11)
		{bcsc[tan^(-1)(b/a)]}" src="http://mathworld.wolfram.com/images/equations/ExponentialFunction/Inline25.gif" style="height:36px; width:127px" />	(12)
		{asec[tan^(-1)(b/a)]}." src="http://mathworld.wolfram.com/images/equations/ExponentialFunction/Inline28.gif" style="height:36px; width:131px" />	(13)

The exponential function has continued fraction

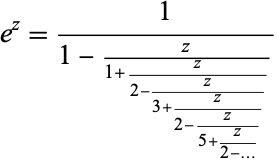(14)

(Wall 1948, p. 348).

Min   Max       Re       Im

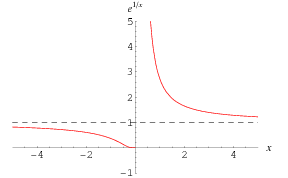
The above plot shows the function 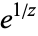 (Trott 2004, pp. 165-166).

Integrals involving the exponential function include

			(15)
			(16)

(Borwein et al. 2004, p. 55).

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Exponential Function." §4.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 69-71, 1972.

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 217, 1987.

Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.

Finch, S. "Linear Independence of Exponential Functions." http://algo.inria.fr/csolve/sstein.html.

Fischer, G. (Ed.). Plates 127-128 in Mathematische Modelle aus den Sammlungen von Universitäten und Museen, Bildband.Braunschweig, Germany: Vieweg, pp. 124-125, 1986.

Krantz, S. G. "The Exponential and Applications." §1.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 7-12, 1999.

Spanier, J. and Oldham, K. B. "The Exponential Function 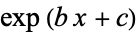" and "Exponentials of Powers 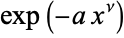." Chs. 26-27 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 233-261, 1987.

Trott, M. "Elementary Transcendental Functions." §2.2.3 in The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.

Wall, H. S. Analytic Theory of Continued Fractions. New York: Chelsea, 1948.

Yates, R. C. "Exponential Curves." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 86-97, 1952.

Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, 1995.