
Complex Argument
 المؤلف:
Abramowitz, M. and Stegun, I. A.
المؤلف:
Abramowitz, M. and Stegun, I. A.
 المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
 الجزء والصفحة:
...
الجزء والصفحة:
...
 18-10-2018
18-10-2018
 1129
1129
Complex Argument
A complex number 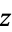 may be represented as
may be represented as
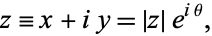 |
(1)
|
where 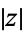 is a positive real number called the complex modulus of
is a positive real number called the complex modulus of 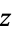 , and
, and 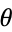 (sometimes also denoted
(sometimes also denoted 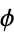 ) is a real number called the argument. The argument is sometimes also known as the phase or, more rarely and more confusingly, the amplitude (Derbyshire 2004, pp. 180-181 and 376).
) is a real number called the argument. The argument is sometimes also known as the phase or, more rarely and more confusingly, the amplitude (Derbyshire 2004, pp. 180-181 and 376).
The complex argument of a number 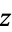 is implemented in the Wolfram Language as Arg[z].
is implemented in the Wolfram Language as Arg[z].
The complex argument can be computed as
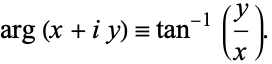 |
(2)
|
Here, 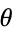 , sometimes also denoted
, sometimes also denoted 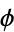 , corresponds to the counterclockwise angle from the positive real axis, i.e., the value of
, corresponds to the counterclockwise angle from the positive real axis, i.e., the value of 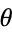 such that
such that 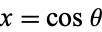 and
and 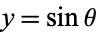 . The special kind of inverse tangent used here takes into account the quadrant in which
. The special kind of inverse tangent used here takes into account the quadrant in which 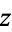 lies and is returned by the FORTRAN command ATAN2(y, x) and the Wolfram Language function ArcTan[x, y], and is often (including by the Wolfram Language function Arg) restricted to the range
lies and is returned by the FORTRAN command ATAN2(y, x) and the Wolfram Language function ArcTan[x, y], and is often (including by the Wolfram Language function Arg) restricted to the range 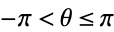 . In the degenerate case when
. In the degenerate case when 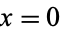 ,
,
![theta=<span style=]() {-1/2pi if y<0; undefined if y=0; 1/2pi if y>0. " src="http://mathworld.wolfram.com/images/equations/ComplexArgument/NumberedEquation3.gif" style="height:78px; width:151px" /> {-1/2pi if y<0; undefined if y=0; 1/2pi if y>0. " src="http://mathworld.wolfram.com/images/equations/ComplexArgument/NumberedEquation3.gif" style="height:78px; width:151px" /> |
(3)
|
Special values of the complex argument include
From the definition of the argument, the complex argument of a product of two numbers is equal to the sum of their arguments,
It therefore follows that
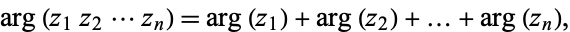 |
(13)
|
giving the special case
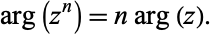 |
(14)
|
Note that all these identities will hold only modulo factors of 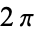 if the argument is being restricted to
if the argument is being restricted to ![theta in (-pi,pi]](http://mathworld.wolfram.com/images/equations/ComplexArgument/Inline43.gif) .
.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 16, 1972.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
Krantz, S. G. "The Argument of a Complex Number." §1.2.6 n Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 11, 1999.
Silverman, R. A. Introductory Complex Analysis. New York: Dover, 1984.
 الاكثر قراءة في التحليل العقدي
الاكثر قراءة في التحليل العقدي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


