Line Integral
المؤلف:
Krantz, S. G.
المصدر:
"The Complex Line Integral." §2.1.6 in Handbook of Complex Variables. Boston, MA: Birkhäuser
الجزء والصفحة:
...
21-8-2018
2598
Line Integral
The line integral of a vector field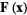 
on a curve 
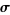is defined by
 |
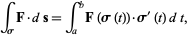(1)
|
where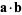 
denotes a dot product. In Cartesian coordinates, the line integral can be written
 |
(2)
|
where
![F=[F_1(x); F_2(x); F_3(x)].](http://mathworld.wolfram.com/images/equations/LineIntegral/NumberedEquation3.gif) |
(3)
|
For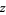 
complex and 
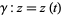a path in the complex plane parameterized by ![t in [a,b]](http://mathworld.wolfram.com/images/equations/LineIntegral/Inline6.gif)
,
 |
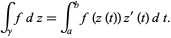(4)
|
Poincaré's theorem states that if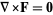 
in a simply connected neighborhood 
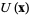of a point 
, then in this neighborhood,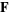 
is the gradient of a scalar field 
,
 |
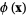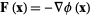(5)
|
for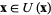 
, where 
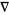is the gradient operator. Consequently, the gradient theorem gives
 |
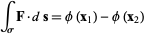(6)
|
for any path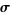 
located completely within 
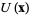, starting at 
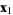and ending at 
.
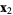This means that if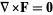 
(i.e., 
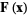is an irrotational field in some region), then the line integral is path-independent in this region. If desired, a Cartesian path can therefore be chosen between starting and ending point to give
 |
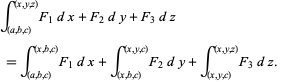(7)
|
If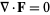 
(i.e., 
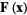is a divergenceless field, a.k.a. solenoidal field), then there exists a vector field 
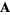such that
 |
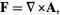(8)
|
where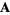 
is uniquely determined up to a gradient field (and which can be chosen so that 
).
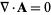REFERENCES:
Krantz, S. G. "The Complex Line Integral." §2.1.6 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 22, 1999.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
