

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
The Quadratic Formula
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
www.almerja.com
الجزء والصفحة:
...
9-3-2017
2221
What is the quadratic formula?
The quadratic formula is used to solve a very specific type of equation, called a quadratic equation. These equations are usually written in the following form:
Ax2 + Bx + C = 0
Quadratic Equations
We may use the quadratic formula to solve quadratic equations, which are second order polynomials (the highest exponent is two). In simple terms, that means that there's an x2 term, but no x3 or x4terms etc.
They only have one variable, which is often named x. In the equation shown above, the letters a,b,c represent numbers (constants). For example, this is a typical quadratic equation:
ax2 + bx + c = 0
2x2 - 8x + 7 = 0
Notice that I've replaced "a" with 2, "b" with -8, and "c" with 7. Now, how would you solve that equation for x? There's no way to easily manipulate that equation into an x= form. This is where the quadratic formula comes in handy.
The Quadratic Formula
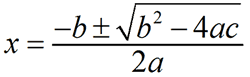
It looks really complicated, I know. Once you use it a lot you'll learn the formula by heart, but until then keep trying. Actually using it isn't that hard -- just plug in your numbers step-by-step. Just insert the values for a,b,c and you'll be left with two possible answers for x.
Confused? Try to follow this example:
Example:
Solve this equation for x: x2 - 4x + 4 = 0
Solution:
What are the three coefficients (a,b,c)? Remember that "a" is the coefficient in front of the x2 term, b is the coefficient in front of x, and c is that constant at the end.
Therefore, for this equation, a=1, b= -4, and c= 4.
Plug those values into the quadratic formula and solve for x:
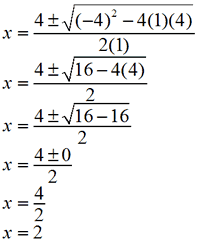
Notice what happened to the +/- sign in that example. Because we were adding or subtracting 0, BOTH answers are the same. There are actually TWO answers for any quadratic formula, and in this case they are both 2.
Check out another example using the quadratic formula where there are two different answers:
Example:
Solve for x: x2 + 2x = 3
Solution:
This equation isn't in the proper form -- we first need to subtract 3 from each side so there's a 0 on the right:
x2 + 2x - 3 = 0
Now we can just use the quadratic formula to get our answers, given that a=1, b=2, c= -3:
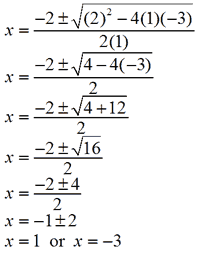
As you can see, we got two answers for this equation. It might seem weird that x could be two different answers, but if you look at the graph for this type of equation, it makes sense. Quadratic equations look like parabolas when graphed, and a parabola can certainly cross the y axis twice (meaning y=0 in two places).
What if you get a negative number inside the square root? That means there are NO possible real answers. This is also possible, and something to look out for. If b2 is not larger than 4ac then the term will be negative and you have no real answers for x.
The quadratic formula is complicated, but if you just follow the steps you'll have no trouble. Memorizing it might take a while, but it's something that will come in very handy.
 الاكثر قراءة في مواضيع عامة في الجبر
الاكثر قراءة في مواضيع عامة في الجبر
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















