البلازما كسائل ناقل

ان الخاصية الاساسية للبلازما تكمن في ان وسطاها المتحرك ذو مقدرة على نقل التيار الكهربائي لذلك فان النموذج الابسط للبلازما هو نموذج السائل الناقل حيث لا ينظر الى حركة الجسيمات المفردة في هذا النموذج بل تعتبر البلازما كوسط مصمت بشكل يشبه ما هو عليه الحال في الهدروديناميك الهادي وفي تقريب ابسط يمكن ان لا نفرق بين السائل والغاز وبغياب التأين يكون الفرق بين هاتين الحالتين للمادة مقتصرا على قابليتهما للانضغاط تظهر اثناء الجريان اذا ما كانت السرعة التي يتم بها تقارب سرعة الصوت لذلك فان الهدروديناميك هو علم عن حركة السائل والغازات ايضا ما دامت ذات سرعة جريان صغيرة بالمقارنة مع سرعة الصوت . لذلك فان الهدروديناميك هو علم عن حركة السوائل والغازات ايضا ما دامت ذات سرعة جريان صغيرة بالمقارنة مع سرعة الصوت. تختلف البلازما ( اي الغاز الناقل) عن السائل الناقل ليس فقط بقابليتها للانضغاط بل وبدرجات حرية اخرى ايضا ذات صلة بانفصال الشحنات لذلك فان للنموذج الهدروديناميكي مجال تطبيق اضيق ومن الجدير بالذكر انه ليست سرع الجريان وحدها التي يجب ان لا تكون كبيرة جدا بل تواترت الاهتزازات المأخوذة كلها حيث ان العمليات البطيئة الى حد كاف في البلازما هي التي يمكن ان توصف بنموذج السائل الناقل وفي هذا النموذج لا يوجد تمييز بين البلازما والمعدن السائل من امثال الزئبق او الصوديوم المنصهر ويمكن تبسيط مسألة الناقلية بأخذ حالة حدية للناقلية المثالية اي اهمال المقاومة الكهربائية للبلازما كليا حيث يسعى حقل الناقلية الى اللانهاية في هذه الحالة الحدية تظهر اكثر السمات التي تميز السائل الناقل عن السائل العادي وتأخذ كافة القوانين شكلا بسيطا ومن المريح عموما الانطلاق من الحالة ذات الناقلية المثالية ومن ثم اضافة التصحيح عليها.

تتميز حركة السائل الناقل بأنها يمكن ان تتأثر بالحقل المغنطيسي ويسمى العلم الذي يتناول حركة السوائل الناقلة الهدروديناميك المغنطيسي.

تكمن طريقة الهدروديناميك المغنطيسي في الحل المشترك لمعادلات تحريك السوائل (الهدروديناميك) ومعادلات التحريك الكهربائي (الالكتروديناميك) ولن نعرف هنا الجملة الكبيرة جدا لهذه المعادلات وانما سنقصر على ذكر نتائج الحل النهائية وهذه تجمل على شكل ثلاثة قوانين اساسية للهدروديناميك المغنطيسي:

• قانون الحقل المغناطيسي المتجمد .
• قانون الضغط المغنطيسي .
• قانون انتثار الحقل المغنطيسي.

يعود القانون الاول والثاني الى الحالة الحدية للناقلية المثالية، في حين يقيم القانون الثالث حدود تطبيق هذه الحالة الحدية.

يعد قانون الحقل المغناطيسي المتجمد نتيجة مباشرة الى قانون التحريض الكهرطيسي في حالة ناقل مثالي وطبقا لقانون التحريض اذا تقاطع ناقل اثناء حركته مع خطوط القوى المغنطيسية فانه تتحرض فيه قوى محركة كهربائية. لكن في الناقل المثالي حيث الناقلية لا منتهية، ومهما كانت القوى المحركة الكهربائية صغيرة فأنها يجب ان تحدث تيارا لا نهاية لكبره وهذا غير ممكن وبالتالي يجب على حركة ناقل مثالي ان تحدث بحيث لا يتقاطع مع خطوط القوى المغناطيسي. واذا جعلنا ناقلا مثاليا يتحرك عبر حقل مغناطيسي بشكل عمودي عليه فانه سوف يجتذب اليه خطوط القوى المغنطيسية.

اذا اثر حقل كهربائي على ناقل يمكن ان يحدث فيه تيار باتجاهه والتيار في الناقل المثالي يجب ان يحرك الناقل عموديا على الحقل المغنطيسي المطبق وبسرعة تجعله يولد فعلا يتعاكس تماما مع فعل القوة المحركة الكهربائية المتولدة بالتحريض ويلغيه مثل هذه الحركة تدعى بالحركة الانجرافية وتدعى سرعته بالسرعة الانجرافية. في الحركة الانجرافية تتحرك الخطوط المغنطيسية والناقل في آن معا. وهكذا فان قانون الحقل المتجمد يتطابق مع مفهوم الحركة الانجرافية وبالتفصيل سوف نتكلم عن الحركة الانجرافية للجسيمات المفردة في البلازما في نموذج الجسيمات المستقلة حيث سنرى بم تتعلق هذه السرعة الانجرافية.

تحدثنا حتى الان عن الناقل الخطي. ولكن بما اننا نتعامل مع سائل فانه يمكننا فصل خط من السائل مرتبط بجسيمات معينة من المادة يقول قانون التجمد على انه في حالة الناقلية المثالية عندما يتحرك خط السائل عبر حقل مغنطيسي بشكل يتعامد فيه منحني الحركة مع الخطوط فان الخط لا يمكنه ان يتقاطع مع خطوط القوة وهذا يعني ان الحقل يجب ان يتحرك مع السائل وكأنه متجمد عليه وبكلام اخر يمكن القول بان خطوط القوة المغنطيسية ملتصقة على جسيمات المادة اذا كان قانون التجمد صحيحا فان حركة السائل تكون خاضعة في كل نقطة لسرعة الانجراف الخاصة بها ويرتبط قانون التجمد على نحو وثيق بالقانون الاساسي الثاني للهدروديناميك المغنطيسي الذي هو قانون الضغط المغنطيسي فحسب قوانين التحريك الكهربائي اذا تغيرت شدة الحقل المغنطيسي باتجاه يعامد خطوط القوة المغنطيسية فانه ينشأ تيار كهربائي يجري باتجاه متعامد مع كلا الاتجاهين السابقين لكن الناقل الذي يمر فيه تيار يعامد الحقل المغنطيسي سوف يخضع من جانب هذا الحقل لقوة تعامد التيار والحقل تدعى بالقوة المحركة الثقالية (Pandermotor force) .

اذا كانت كثافة هذا التيار معلومة فانه من السهل حساب قيمة هذه القوة . وهي متناسبة مع جداء شدة الحقل المغنطيسي H بكثافة التيار المار عبر الحقل (عموديا عليه) (وفي جملة الوحدات الغاوسية) تكتب:

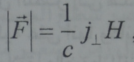
لكن اذا ما عبر عن التيار بدلالة الحقل المغنطيسي فانه باختفاء التيار يمكن النظر الى نفس القوة ليس كقوة محركة ثقالية وانما كقوة ضغط مغنطيسي.

وحسب قوانين التحريك الكهربائي اذا كان الحقل المغنطيسي متجها وفق المحور z ويجري تيار وفق المحور المعامد x كثافة J هو كثافة تيار الناقلية فقط. وبالتعبير عن هذا التيار بواسطة مشتق الحقل المغنطيسي ومن ثم التعويض في عبارة القوة المحركة الثقالية نجد:

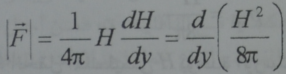
وعند الاهتمام باتجاه القوة وليس فقط بمقدارها فانه يمكن كتابة هذه العلاقات بالشكل المتجه:

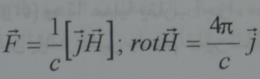
من هنا نجد :

واذا تغير الحقل المغنطيسي فقط وفق اتجاه يعامد اتجاهه يكون:

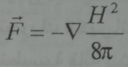
يعني الرمز ∇  التدرج ، أي المشتق وفق الاتجاه.

تبين الحسابات ان القوة المحركة الثقالية تكون باتجاه يتوافق دائما مع اتجاه تناقص الحقل المغنطيسي ويعبر عنها بشكل يماثل عبارة قوة الضغط اذا اعتبر المقدار:

P_M=H²/8_π 

يلعب دور الضغط حيث يفضل النظر الى هذا المقدار على انه ضغط مغنطيسي والنظر الى القوة المحركة الثقالية على انها وكأنها قوة الضغط المغنطيسي.

تمثل النسبة بين ضغط غاز البلازما والضغط المغنطيسي فيها ميزة عددية هامة من ميزات البلازما . هذا العدد اللابعدي اصطلح على ترميزه بالحرف الاغريقي β  

P/P_M = 8πnT/H² = β

يعد استخدام مفهوم القوة المحركة الثقالية او الضغط المغنطيسي طريقتان للتعبير عن قوانين فيزيائية واحدة وكلتاهما صحيحتان ومقبولتان وتؤديان الى نتائج متطابقة.

يمكن عرض هذه المسألة من وجهة نظر اخرى فكما هو معلوم في الالكتروديناميك يولد الحقل المغنطيسي في الفضاء ضغطا مساويا لكثافة الطاقة المغنطيسية أي ضغطا يتناسب طردا مع مربع شدة الحقل المغنطيسي وفق العبارة:

P_M= H²/8π 

اذا قدرن شدة الحقل المغنطيسي H بوحدة الارسند (او ما يساويها في الفضاء الخالي من تحريض مغنطيسي B مقدار بالغاوس) فالضغط سيقدر في الوحدات السغثية بوحدة (erg/cm³) وهذا عمليا يقارب اجزاء من مليون من الضغط الجوي لكن هذا الضغط لن يؤثر على جسم غير ناقل لذلك فهو لا يحسب في الهدروديناميك العادي في الواقع ينفذ الحقل المغنطيسي عبر جسم غير ناقل بكل حرية ويمكن ان يؤثر الضغط فقط على حاجز لا يخرقه الحقل. وينتج عن قانون التجمد انه في ناقل مثالي وباتجاه عمودي على خطوط القوة لا يستطيع الحقل المغنطيسي ان ينفذ وهذا يعني انه وفق هذا الاتجاه يجب ان تؤثر قوى الضغط المغنطيسي بشكل كامل على الناقل المثالي.

 وعند النظر في حركة السائل المثالي او بلازما الغاز فانه يلزم الى جانب الضغط العادي للمادة اخذ الضغط المغنطيسي بالحسبان ايضا.

وعندئذ لابد من الاخذ في الاعتبار الشرطين التاليين:

اولا: ان الضغط المغنطيسي لا يؤثر الا باتجاه عمودي على خطوط القوة المغنطيسية أي انه غير متناحي معها.

وثانيا: ان الضغط المغنطيسي يؤثر في حالة الناقلية المثالية الحدية (اللامنتهية) على نحو كامل. اما في حالة الناقلية المنتهية فان قانون التجمد يتعطل ويتسرب الحقل المغنطيسي تدريجيا عبر سطح الجسم. ويكون الجسم ذا مقدرة على تحسس الضغط المغنطيسي فقط خلال زمن صغير مقارنة بزمن مثل هذا التسرب او كما يقال مقارنة بزمن انتثار الحقل المغنطيسي ولكن عند تفاعل طويل الامد تتم معادلة فعل الضغط المغنطيسي ويتوقف عن التاثير وذلك بشكل مماثل تماما لعدم تأثير ضغط الهواء على منخل النوافذ، اما مقدار معدل تسرب الحقل المغنطيسي فانما يعين وفق القانون الثالث الذي يدعى قانون انتثار الحقل المغنطيسي وهذا يحصل عليه اذا حلت معادلات الهدروديناميك المغنطيسي وقانون اوم العادي في ان معا وينص قانون الانتثار على ان كثافة الكهربائي  j  تكون متناسبة مع شدة الحقل الكهربائي E:

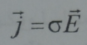
ويدعى عامل التناسب σ  بالناقلية ومن هنا يحصل من اجل تسرب الحقل المغنطيسي على معادلة مطابقة لمعادلة الانتثار العادية ويبدو معامل انتثار الحقل المغنطيسي D_M متناسا عكسيا مع الناقلية σ  فمن اجل الناقل المثالي نجد D_{M → O}  , _∞→ σ من المناسب اتباع جمل احداثيات متناظرة او غاوسية التي يعبر فيها عن المقادير الكهربائية بوحدات CGSE وعن المقادير المغنطيسية بوحدات CGSM فيكون للناقلية σ بعد مساو الى مقلوب الزمن في هذه الجملة (وهو بعد التواتر) ويعبر عن معامل انتثار الحقل المغنطيسي في هذه الحالة بالعلاقة:

 , σπ D_M= C²/ 4   

حيث c سرعة التي تدخل في العلاقات كنسية لوحدات الكهربائية الساكنة الى الوحدات الكهرطيسية ويكون دوما لمعامل الانتثار البعد cm²/ sec .

هذا ويخضع انتثار الحقل المغنطيسي لقوانين العمليات العشوائية الاعتيادية، والتي سيجري الحديث عنها فيما بعد . ان عمق التوغل خلال زمن t هو من مرتبة:

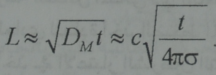
وخلال زمن قصير t يفلح الحقل المغنطيسي وكذلك التيار بالتوغل فقط عبر طبقة سطحية رقيقة من الناقل سماكتها وهي ما تدعى الطبقة القشرية (من الكلمة الانكليزية skin جلد او قشرة). وبالتالي يتوغل الحقل والتيار الى عمق معطى L خلال زمن مرتبة:

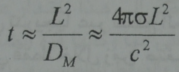
والذي يدعى زمن التوغل القشري .

ويتوغل التيار المتناوب في الناقل فقط خلال نصف الدور. لذلك فان التيار عالي التواتر يمر فقط طبقة جلدية رقيقة على سطح الناقل. ويحصل على ثخانة هذه الطبقة الجلدية المستقرة، اذا ما تم استبدال t بمقدار مقلوب التواتر (اصطلح على اخذ /ω  t= 2π/ حيث ω  التواتر الدائري).