ثرموديناميك البلازما

الثرموديناميك هو علم يدرس صفات وسلوك الاجسام الواقعة في حالة التوازن الحراري تؤدي التصادمات بين الجسيمات في الوسط الكثيف الى تحقق التوازن الحراري سريعا على عكس خالات البلازما المتخلخلة حيث تصبح التصادمات نادرة وبالتالي يمتد التأين حيث يتناقص احتمال التصادم فيها بين الجسيمات بسرعة مع ارتفاع درجة الحرارة لهذا السبب يمكن القول بأن البلازما الباردة والكثيفة وعلى الاخص البلازما ضعيفة التاين تكون عادة في حالة توازن حراري ولذا يمكن توصيف هذه البلازما بواسطة الترموديناميك وعلى العكس تكون البلازما المتخلخلة والتامة التاين والحارة في حالة عدم التوازن لفترات طويلة وفي هذه الحالات يصبح الترموديناميك غير صالح لوصف البلازما .

يلعب مفهوم درجة الحرارة دورا اساسيا في الثرموديناميك وهي مقدار يميز توزع الطاقة بين جسيمات الجملة التي هي في حالة البلازما الالكترونات والايونات .

يعبر عن توزع الطاقة في حالة التوازن الحراري بتابع انسيابي معين اعطي شكله لاول مرة من قبل ماكسويل مثل هذا التوزع يدعى توزع ماكسويل (الشكل 1) .

وهو منحن يبين بدلالة قيم الطاقة تغير اعداد الجسيمات التي تحمل طاقة واقعة في مجال طاقي ضيق تدخل درجة الحرارة في هذه التابعية كوسيط اي ان شكل هذا المنحني يتغير مع تغير درجة الحرارة وكلما ارتفعت درجة الحرارة ازداد عدد الجسيمات التي تحمل طاقات اعلى وفيما يخص درجة الحرارة فانها تتعين بالقيمة الوسطية للطاقة الحرارية التي تصيب درجة حرية واحدة من حركة الجسيمة فاذا قيست درجة الحرارة بالوحدات العادية درجات الحرارة المطلقة (الكفن K ) تكون الطاقة الوسطى التي تعود الى كل درجة من درجات الحرية مساوية KT ½ ،حيث K .

ثابت بولتزمان (او ثابت الغازات العام مقسوما على آفوغادرو).

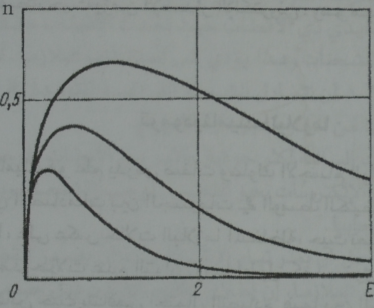
الشكل (1) توزيع ماكسويل

وفي الجسيمات شبه الحرة (البسيطة) والتي لا تملك درجات حرية داخلية ترتبط الطاقة الحرارية كلها بالحركة الانتقالية ولما كان لدى كل جسيمة فيها ثلاث درجات للحرية (الحركة وفق ثلاثة اتجاهات في الفراغ). تكون الطاقة الوسطى لكل من هذه الجسيمات مساوية KT 2/3 يمكن للالكترونات والايونات ان تتحرك حركة انتقالية فقط في حالة البلازما المتأينة كليا (ليس لديها درجات حرية داخلية) لذلك فان الطاقة الحرارية للبلازما المتوازنة والمتأينة كليا تعطى بكل بساطة بالعلاقة KT (2/3) =E متوسط الطاقة الحركية للجسيمة الواحدة . اذا كانت طاقة التاثير المتبادل بين الجسيمات صغيرة بالمقارنة مع الطاقة الحرارية فان البلازما ستتصرف بالمفهوم الترموديناميكي كالغاز المثالي عندها تتطابق الطاقة الكلية للبلازما عمليا مع طاقتها الحرارية ويعطي ضغطها بمعادلة الحالة للغاز المثالي على النحو التالي:

P=(n_e – n_i)kt 

حيث n_e و n_i تركيز الالكترونات والايونات على التوالي .

تقدر الطاقة في الفيزياء الذرية بوحدة الالكترون – فولت او e v . وهي الطاقة التي يكتسبها الكترون عند اجتيازه لفرق كمون قدره 1v وهي مقدار صغير القيمة جدا يساوي 1ev = 1.6×10 ^{– 12} .

ان عدد الالكترونات في كمية المادة المنظورة كبير جدا فاذا اعطيت كل ذرة في الجزيء الغرامي (مول واحد) من المادة طاقة قدرها 1ev فانه في الوحدات الحرارية يكون الجزيء الغرامي قد اكتسب 23050 حريرة.

من الانسب ايضا ان تقاس درجة الحرارة بالوحدات الطاقية. عندها يفهم من درجة الحرارة المقدار KT الذي يميز طاقة الحركة الحرارية للذرات والجزيئات⁽¹⁾.

وعند تقدير درجة الحرارة بالوحدات الطاقية تختزل علاقات الترموديناميك، حيث يزول ثابت بولتزمان منها. ويعبر عن طاقة الحركة الانتقالية من اجل جسيمة واحدة ببساطة وفق T (3/2) وتصبح السعة الحرارية عددا بلا وحدة قياس (مقدارا لا بعديا). عادة يقبل الالكترون- فولت كوحدة طاقية لقياس درجة الحرارة من اجل التحويل الى درجات تستخدم العلاقة 1ev = 11600k (أي ان كل طاقة حرارية قدرها 1evيقابلها درجة حرارة قدرها 11600k).

اما درجات الحرارة المطلوبة لتحقيق التفاعلات النووية الحرارية فهي مرتفعة لدرجة انه لاجلها تعتمد وحدة قياس اكبر بـ 1000مرة الا وهي الكيلو الكترون – فولت ورمزه (  (kevحيث ان 1ke= 1.16×10⁷k.

ويعطي ضغط البلازما بالعاقة: p= 1.6×10^-12(n_e+n_i)T حيث T درجة الحرارة (مقدرة بالالكترون – فولت) :  n_e ,n_iتراكيز الالكترونات والايونات معبر عنها بعدد الجسيمات في 1cm³ والضغط  P مقدر بوحدة   dyn/cm² وفق والجملة السغثية اي erg/cm³ . للانتقال الى الوحدات العملية لقياس الضغط- جو ( (atmاو مليمتر زئبقي​ (mmHg) او (torr)- لابد من استخدام امثال التحويل التالية:

1atm≈10⁶ erg/ cm³

1mmHg≈ 1/760 atm ≈ 1.3×10³ erg/cm³

من هنا نجد

P = 1.6×10 ^-18 (n_e + _ni)T ≈atm

≈1.22 × 10 ^-15(n_e + n_i)T mmHg.

وبأخذ درجة الحرارة الغرفة 300K ≈ 1/40 ev  نجد :

P = 3.1 × 10 ^-17 (n_e + n_i) mmHg

لنبحث في شروط تطبيق هذه العلاقة البسيطة عند قيم منخفضة جدا للكثافات لا تكون البلازما في حالة توازن حراري ويصبح مفهوم درجة الحرارة نفسه غير مقبول.

في مثل هذه الظروف من السهل الوقوع في الخطأ اذا ما جرى الحديث عن درجة حرارة البلازما يمكن اخذ مثال تعليمي على ذلك من تاريخ الابحاث النووية الحرارية.

منذ سنوات عديدة جرى في انكلترا بناء منشأة زيتا ZETA لتسخين وحصر البلازما والتي فيها – كما افترض في البدء- تم بلوغ درجات حرارة عالية . واستخدم لقياس درجة الحرارة توسع الخطوط الطيفية التي تصدر عن الايونات الثقيلة الموجودة في البلازما بصفة شوائب صغيرة .

وعند اخذ القياس على الخطوط الصادرة عن الايونات المختلفة وجد ان درجات الحرارة البلازما المقيسة تزداد كلما كبرت شحنة الايون ذلك لان البلازما ليست في حالة توازي وان الجسيمات المختلفة تتحرك في البلازما بطاقات مختلفة وبالتالي فان الحديث هنا درجة حرارة معينة لهذه البلازما ليس ذا معنى .

وعند كثافات اعلى من الممكن ان تتحقق حالة من التوازي الحراري الجزئي فمثلا هذه الحالات يقال ان للبلازما درجتا حرارة درجة , درجة حرارة طولية وهي ناتجة عن الحركة على طول خطوط القوة المغنطيسية ودرجة حرارة عرضية ناتجة.

عن الحركة العرضية المتعامدة مع خطوط القوة مثل هذه الظاهرة التي تكون فيها صفات المادة مختلفة باختلاف الاتجاه تدعى بظاهرة اللاتناحي. اصطلح على اعتبار الاتجاه الموافق للحقل معبرا عنه بالرمز II والاتجاه المتعامد مع الحقل بالرمز    ┴ ووفقا لذلك يرمز لدرجتي الحرارة بـ T_II، T┴ ويقابلها الضغطان P_II و P_┴ حيث P_II ≠ PI.

وبالمثل فان البلازما المتخلخلة الموضوعة في حقل مغنطيسي تعاني ايضا من اللاتتاحيفي الضغط ومع تزايد الكثافة يسهل التبادل الطاقي بين درجات الحرية المختلفة وبتقارب اللاتتاحي الحراري او الضغطي حتى التساوي. ولعل اكثر التبادلات الطاقية صعوبة هي تلك التي تحصل ما بين الالكترونات والايونات وهذا يعود الى الفرق الكبير ما بين فالإلكترون المتصادم مع ايون يرتد عنه كما ترتد كرة التنس عن سيارة شاحنة كبيرة دون ان يتبادلا الطاقة تقريبا . لذلك تبقى درجة حرارة الالكترونات T_e ضمن مجال واسع من القيم مختلفة عن درجة حرارة الايونات T_i.  والبلازما ذات درجات الحرارة الالكترونية والايونية المختلفة تقدم مثالا اضافيا عن التوازن الثرموديناميكي الجزئي ويمكن النظر الى البلازما على انها مزيج من غازين : الكتروني وايوني وكل غاز منهما يقع في توازن حراري بمفرده (وان توزع السرعات سواء داخل الغاز الالكتروني او داخل الغاز الايوني هو توزع ماكسويلي) لكن هذين الغازين لا يكونان دوما في حالة توازن فيما بينهما.

عند كثافة مرتفعة الى حد كاف ينبغي ان تكون البلازما واقعة في حالة توازن ترموديناميكي كلي وعندئذ تتساوى درجتا الحرارة الالكترونية والايونية وان زمن بلوغ التوازن يدعى زمن الاسترخاء الذي سيأتي الحديث عنه فيما بعد .(يتناول الترموديناميك الحالات فقط وليست عمليات بلوغها). لكن عند الرفع المتلاحق للكثافة يمكن ان تغير البلازما صفاتها الترموديناميكية وبالتالي يمكن ان تتوقف البلازما عن السلوك سلوك الغاز المثالي وهذا الحيود عن قوانين الغازات المثالية مرتبط بظاهريتين جديدتين تلاحظان عند الكثافات الكبيرة هما : التفاعل الكهربائي الساكن والانطباق (degeneracy ) .

وعند الكثافة الكبيرة تصبح طاقة البلازما معرفة ليس فقط بالطاقة الحركية للجسيمات بل بالطاقة الكامنة لتفاعلها ايضا. تكون كل جسيمة مشحونة في البلازما محاطة بجسيمات تتزايد مع الكثافة لها ذات الشحنة المعاكسة بالإشارة والتي تحجب الحقل الكهربائي للجسيمة وتكون المسافة التي يحصل عندها الحجب من مرتبة المقياس الفراغي لفصل الشحنات.

وفي حالة البلازما المكونة من جسيمات مختلفة الشحنات يعطي مدى الحجب 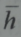 (الذي يدعى ايضا مدى ديباي او مدى الاستقطاب) بدلالة مقياس انفصال الشحنات وذلك بالتعريف بجمع مقاليب مربعات مسافات الفصل h_k بينها وبين الجسيمات ذات الشحنة Z_k أي:

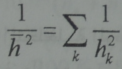
h_kويعطي  مقياس الفصل او التباعد بالعلاقة:

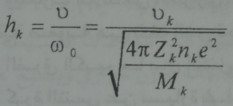
حيث Ʋ تمثل السرعة الوسطية للحركة الحرارية للجسيمات في البلازما الحرارية و _kƲ السرعة الوسطية للجسيمات ذات الشحنة Z_k  ، أي

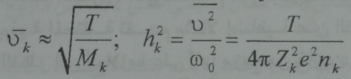
وحيث n_k تمثل تركيز الجسيمات ذات الشحنة Z_k و T تمثل درجة الحرارة بالوحدات الطاقية وعليه يكون في البلازما المتوازنة:

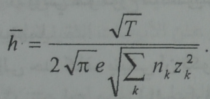
يؤخذ الجمع على كل الجسيمات k الايونات منها والالكترونات حيث تعطي Z بالقيمة (Z=1) ويمكن ادخال المقدار

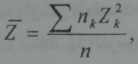
حيث n=n_e + n_i التركيز الكلي لكافة الجسيمات.

مع الاخذ بالاعتبار شرط التعادل الكهربائي فان Z يعتبر قريبا من عدد الشحنة الوسطى للأيونات بعد هذا يمكن كتابة عبارة مدى الحجب بالشكل:

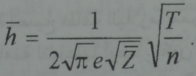
يطول مدى الحجب كلما ارتفعت درجة الحرارة وانخفضت كثافة البلازما واذا ما عبر عن درجة الحرارة بوحدات قياس سهلة عمليا الكترون فولت وعبر التركيز بعدد الجسيمات في   1cm³وعن طول الحجب بالسنتيمترات فان:

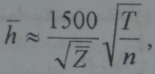
ففي البلازما الكثيفة يكون مدى الحجب حتى في درجات الحرارة العالية صغيرا عندئذ تتناقص طاقة البلازما بسبب التجاذب المتبادل بين كل جسيمة ومحيطها بما يحوي من جسيمات زائدة ذات شحنات معاكسة فاذا ما عبر عن طاقة الجسيمة الواحدة فأنها سوف تنقص بمقدار  EΔ حيث

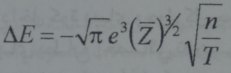
وهو ما يدعي الطاقة الكهروساكنة وهي طاقة سالبة مثلها مثل أي طاقة أي انها مماثلة لطاقة تجاذب جسيمات البلازما المختلفة الشحنة ضمن مدى الحجب وبدلالة نفس وحدات القياس الطاقية يمكن كتابتها بالشكل:

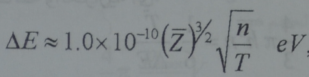
ومنه يمكن ان نعبر عن النسبة بين الطاقة الكهروساكنة والطاقة الحرارية بالعلاقة:

تتصرف البلازما بالمفهوم الترموديناميكي كغاز مثالي ما دامت هذه النسبة صغيرة أي:

1 >> E/TΔ

أي ما دامت الكثافة n منخفضة كفاية ودرجات الحرارة T مرتفعة.

عندما يكون التصحيح المجرى على الطاقة الكهروساكنة اكبر من 1% تسمى الكثافة المقابلة بالحدية وعندئذ نحصل على الحد الادنى لهذه الكثافة بالعلاقة:

 n= 10 ¹⁶(T/Z) ³

فالكثافة الحدية متناسبة مع مكعب درجة الحرارة اما الضغط الموافق لها فهو متناسب مع القوة الرابعة لدرجة الحرارة فمثلا اذا كان Z=1 (بلازما الهدروجين) فعند درجة حرارة 1evيمكن اهمال التجاذب الكهروساكن عندها لا تتجاوز كثافة البلازما 10¹⁶ جسيمة cm³ وضغطها اجزاء المئة من الضغط الجوي اما عند درجة حرارة 10ev

فهذا سيبقى مسموحا حتى كثافة من مرتبة 10¹⁹ جسيمة cm³ وضغوطا حتى 30 جو في حين ان البلازما الباردة الكثيفة تنحرف عن قوانين الغاز المثالي مع العلم ان الباردة هنا يقصد بها بلازما بدرجة حرارة لا تزيد على 10000k.

ان تناقص طاقة البلازما يكون مصحوبا بتناقص في ضغطها وهذا يمكن حسابه وفقا لعلاقات الترموديناميك وما دامت الطاقة الكهروساكنة صغيرة مقارنة مع الطاقة الحرارية فان الضغط ينقص بمقدار:

 E nΔP= 1/3 Δ   

كل العلاقات الواردة من اجل التفاعل الكهروساكن تستخرج من نظرية ديباي.

لذلك فان مدى الحجب h يدعى مدى ديباي والكرة ذات نصف القطرh تدعى كرة ديباي . يمكن القول انه داخل كرة ديباي وحول كل جسيمة تستشعر القوى الكهربائية .

تتمتع نظرية ديباي بطابع احصائي تقريبي وان استخدامها ممكن ضمن شروط هي ان يكون عدد الجسيمات داخل كرة ديباي كبيرا. يمكن التأكد بواسطة العلاقات الواردة اعلاه بان عدد الجسيمات في كرة ديباي يتناسب عكسيا مع النسبة بين الطاقة الكهروساكنة والحرارية أي:

ΔEn= 1/6 ,T/ 4/3π h³     

وهكذا فان كل العلاقات الواردة سابقا من اجل تصحيح الطاقة والضغط من جراء التفاعل الكهروساكن تبقى صالحة فقط في حالة البحث عن الكثافات التي يبقى عندها الترموديناميك مطبقا على البلازما أي ثرموديناميك الغاز المثالي وعند تجاوز هذا الحد نقع ضمن مجال تصبح فيه البلازما كأنها غاز مضغوط او سائل مسخن الى ما فوق درجة الحرارة الحرجة ولا توجد عندئذ قوانين بسيطة قادرة على وصف البلازما من حيث صفاتها الترموديناميكية وهذه صفات غير مدروسة تماما بشكل عام لان حساب التفاعل الجماعي لعدد كبير من الجسيمات فيما بينها امر صعب جدا لكن من السهل ان نشير الى ان القوانين الحدية لترموديناميك البلازما تكون عند كثافات اكثر ارتفاعا . انما تعود الى المجال حيث طاقة البلازما وضغطها يتعينان ليس بالتفاعل الكهروساكن فقط بل بظاهرة فيزيائية اخرى الا وهي الانطباق.

ان الانطباق في غاز الكتروني يعتبر نتيجة مباشرة لاحد المبادئ الاساسية في الفيزياء الكوانتية . الا وهو مبدأ باولي ووفقا لهذا المبدأ فانه في حركة كوانتية واحدة لا يمكن ان يوجد اكثر من الكترون واحد لكي نطبق هذا المبدأ على الغاز من الانسب استخدام فراغ طوري سداسي والذي يعطي الحجم فيه كجداء حجم في الفراغ الاحداثي الثلاثي بالحجم في الفراغ الاندفاعي الثلاثي ايضا:

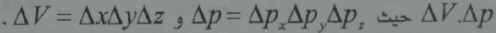
وحيث ان p هو اندفاع الجسيمة أي جداء الكتلة بالسرعة وحيث ان كل حالة كوانتية تشغل في الفراغ الطوري خلية حجما h³ , h هو ثابت بلانك فانه ان تشغل هذه الخلية بإلكترونين لا اكثر يختلفان باتجاه لفهما الذاتي أي السبين.

اذا كانت الكثافة صغيرة فان الاماكن (الخلايا) في الفراغ الطوري تكفي لكل الالكترونات وتزيد وان مبدأ باولي لن يؤثر على صفات البلازما لكن اذا ما ضغطت البلازما فانه يمكن ايصالها الى حالة تكون فيها كل الخلايا مشغولة ولدى الاستمرار في الضغط على البلازما فان الالكترونات تأخذ بالانضغاط في الاندفاع في خلايا ذات طاقة اعلى . وعند الضغط الشديد جدا على البلازما فان طاقة وضغط الغاز الالكتروني سيزدادان بغير سبب درجة الحرارة.

ويستحصل على العلاقات الترموديناميكية من اجل الحالة الحدية للتردي (الانطباق) الكلي ببساطة كلية كما يلي: في الحالة الحدية تكون الحالات مشغولة (الخلايا) حتى بلوغ الاندفاع الاعظمي p_max فاذا كانت البلازما تشغل حجما V في الفراغ العادي فأنها ستشغل في الفراغ السداسي الطوري حجما قدره 4/3 π p³_maxV (حيثP³_MAX 4/3π حجم كرة في فراغ الاندفاع) ويكون عدد الخلايا العنصرية في هذا الحجم هو:

4/3 π P³_max/h³. V   

ويمكن ان تحوي كل خلية على الكترونين بنسبين ذاتيين متعاكسين. ومن هنا فان العدد الكلي للإلكترونات التي يمكن ان تستوعب في الحجم الطوري باندفاعات دون P_max هو :

P³_max/h³.Vπ . .N= 8/3  

وان تركيز الالكترونات أي عدد الالكترونات في وحدة الحجم هو:

P³_max/h³. 8/3. π n= N/V=           

هذا يعني انه اذا كان التركيز الالكتروني n فان الاندفاع الاعظمي هو:

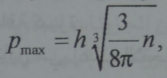
وان الطاقة الحركية الاعظمية تساوي :

(E_max=p²_max/2m =h²/2m .(3/8 π .n.

يتبين من حساب بسيط انه اذا كانت الالكترونات شاغله لكرة في فراغ الاندفاع بكثافة منتظمة فان الطاقة الوسطى لألكترون واحد تعطي بالعلاقة:

E= 3/10. H²/m(3/8 π. n)^2/3 

وحسب قوانين الترموديناميك يعطي الضغط بالعلاقة :

P=2/3. En= 1/5 .h²/m(3/8 π)^2/3 n^5/3

وهي العلاقة الحدية لتروموديناميك البلازما عند كثافات عالية جدا تدعى الطاقة E_MAX بانها طاقة الانطباق او طاقة فيرمي فاذا كانت كبيرة مقارنة بالطاقة الحرارية والطاقة الكهروساكنة فان طاقة وضغط البلازما سوف تتعينان بطاقة وضغط الغاز الالكتروني المتردي. من المفيد ان نشير هنا الى ان الضغط يتناسب طردا مع الكثافة مرفوعة للقوة 5/3 وكذلك الحال عند انضغاط غاز مثالي عادي وفق قانون التحولات المكظومة لكن الطاقة والضغط لا يتعلقان بدرجة الحرارة نهائيا في مجال التردي التام.

__________________________________

(1) اذا توخينا الدقة هذه هي لطاقة المترتبة على درجتي حرية من درجات حرية حركة جسيمة المادة.