This section is devoted to examples of the methods we have derived so far in the treatment of two types of logical problems. Although it is a repetition of material already presented, specific illustrations may help the student to realize the flexibility of Boolean algebra and strengthen his ability to successfully treat problems of an applied nature. The first problem is of a type which arises naturally in writing or interpreting legal documents and insurance contracts. Although the examples given in this text are nonsensical, the methods apply equally well to important problems of a more realistic nature.

EXAMPLE 1. The irascible husband carried his new bride across the threshold and then remarked, "We'll get along fine, Honey, provided you observe the following rules:

"(a) At any meal when you do not serve bread, you must serve ice cream.

"(b) If you serve both bread and ice cream at the same meal, then you must not serve dill pickles.

"(c) If dill pickles are served, or bread is not served, then ice cream must not be served."

The bride was willing to comply, but was a bit confused about how to remember these somewhat involved rules. The problem is to simplify the rules.

First solution. Stating three conditions which must hold simultaneously is equivalent to stating that the conjunction of the three propositions represented must hold. We will form this conjunction and simplify it to an equivalent proposition which is easier to interpret than the original set of three. Denote the simple propositions involved as follows:

b: Bread is to be served.

i:Ice cream is to be served.

p: Dill pickles are to be served.

Now the rules may be translated into the following symbolic expressions:

Forming the conjunction of these propositions, we have

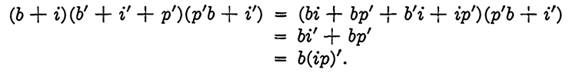
Hence the single rule "always serve bread, and never serve ice cream and pickles together" is equivalent to the three given rules.

Although the preceding method is straightforward, it does not fit in very well with the methods introduced in Chapter (THE ALGEBRA OF SETS) for dealing with conditional equations, even though the problems are essentially the same.  To make this clear, we note that stating a proposition as a premise is equivalent to an assertion that it is true. That is, instead of merely listing p → q, we might equally well write p →q = 1, or p' + q = 1, or pq' = 0. The same information is conveyed in each case, although the last three forms are not propositions. This suggests an alternate solution for Example 1.

Second solution. Using the same notation as before, we now translate the three rules as follows:

Combining these equations, we obtain

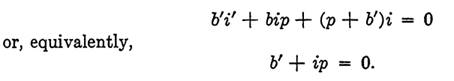
Now, taking complements of both sides, we have

                                                                     b(ip)' = 1,

and this leads to the same final rule as before.

Since p →q is equivalent to pq' = 0, Theorem 10 of Section (Definition and properties of a Boolean algebra) on the transitivity of a has a corollary in the algebra of propositions. This corollary could be worded, if p →q and q → r are known to be true, then it follows that p → r is true. This is equivalent to the statement that                   [(p →q) (q →r)] →(p → r) is a tautology, and hence to the valid argument called the law of syllogism. Sets of premises from which a valid conclusion may be drawn by more than one application of the law of syllogism are called sorites. Syllogisms and sorites may be solved either by using the notations of the algebra of sets, or by using those of the algebra of propositions.

EXAMPLE 2. Suppose that it is desired to form a conclusion from the following premises:

(a) A grouper is a fish.

(b) If an animal is a fish, then it swims well.

(c) An animal is clumsy only if it does not swim well.

(d) All animals are either clumsy or agile.

First solution. Using the terminology of sets, we define the universal set to be the set of all animals and define subsets as follows:

G: the set of all groupers,

F: the set of all fish,

S: the set of all animals that swim well,

C: the set of all clumsy animals,

A : the set of agile animals.

The translations into symbols are then

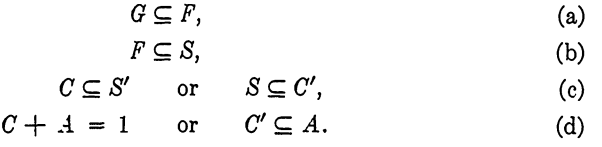
Hence we conclude that G ⊆A or, in words, "all groupers are agile." This is called the -major conclusion. There are other conclusions, called minor conclusions that might also be drawn; for instance, "groupers swim well."

Second solution. Using the terminology of propositions, define propositional symbols as follows:

g: This animal is a grouper.

f : This animal is a fish.

s: This animal swims well.

c: This animal is clumsy.

a: This animal is agile.

The translations are

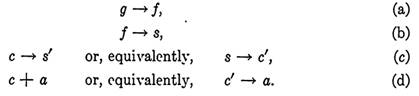
From these we conclude that g →a or, in words, "if this animal is a grouper,  then it is agile." This result is the same as before even though the wording is slightly different.