In applied mathematics physical quantities are represented by two distinct classes of objects. Some quantities, denoted scalars, are represented by real numbers. Others, denoted vectors, are represented by directed line elements: e.g. . Note

that line elements (and therefore vectors) are movable and do not carry intrinsic position information. In fact, vectors just possess a magnitude and a direction, whereas scalars possess a magnitude but no direction. By convention, vector quantities are denoted by bold-faced characters (e.g. a) in typeset documents and by underlined characters (e.g. ) in long-hand. Vectors can be added together but the same units must be used, like in scalar addition. Vector addition can be represented using a parallelogram: =   +  . Suppose that a ≡≡ ,

b ≡ ≡, and c ≡ . It is clear from the diagram that vector addition is commutative: e.g., a + b = b + a. It can also be shown that the associative law holds: e.g., a + (b + c) = (a + b) + c. There are two approaches to vector analysis. The geometric approach is based on line elements in space. The coordinate approach assumes that space is defined by Cartesian coordinates and uses these to characterize vectors. In physics we adopt the second approach because we can generalize it to n-dimensional spaces without suffering brain failure. This is necessary in special relativity, where three- dimensional space and one-dimensional time combine to form four-dimensional space-time. The coordinate approach can also be generalized to curved spaces, as is necessary in general relativity. In the coordinate approach a vector is denoted as the row matrix of its components along each of the Cartesian axes (the x, y, and z axes, say):

     (1.1)

Here, ax is the x-coordinate of the ''head" of the vector minus the x-coordinate of its ''tail". If  a ≡ (a_x, a_y, a_z) and b ≡ (b_x, b_y, b_z) then vector addition is defined

         (1.2)

If a is a vector and n is a scalar then the product of a scalar and a vector is defined

 (1.3)

It is clear that vector algebra is distributive with respect to scalar multiplication: e.g., n(a + b) = na + nb. Unit vectors can be defined in the x, y, and z directions as i ≡ (1, 0, 0), j ≡ (0, 1, 0), and k ≡ (0, 0, 1). Any vector can be written in terms of these unit vectors

     (1.4)

In mathematical terminology three vectors used in this manner form a basis of the vector space. If the three vectors are mutually perpendicular then they are termed orthogonal basis vectors. In fact, any set of three non-coplanar vectors can be used as basis vectors.

Examples of vectors in physics are displacements from an origin

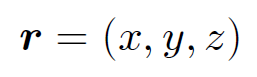 (1.5)

and velocities

   (1.6)

Suppose that we transform to new orthogonal basis, the xʹ, yʹ, and zʹ axes, which are related to the x, y, and z axes via rotation through an angle θ around the z-axis. In the new basis the coordinates of the general displacement r from the

origin are (xʹ, yʹ, zʹ). These coordinates are related to the previous coordinates via

       (1.7)

We do not need to change our notation for the displacement in the new basis. It is still denoted r. The reason for this is that the magnitude and direction of r are independent of the choice of basis vectors. The coordinates of r do depend on the choice of basis vectors. However, they must depend in a very specific manner [i.e., Eq. (1.7) ] which preserves the magnitude and direction of r. Since any vector can be represented as a displacement from an origin (this is just a special case of a directed line element) it follows that the components of a general vector a must transform in an analogous manner to Eq. (1.7). Thus,

 (1.8)

with similar transformation rules for rotation about the y- and z-axes. In the coordinate approach Eq. (1.8) is the definition of a vector. The three quantities (a_x, a_y, a_z) are the components of a vector provided that they transform under rotation like Eq. (1.8). Conversely, (ax, ay, az) cannot be the components of a vector if they do not transform like Eq. (1.8). Scalar quantities are invariant under transformation. Thus, the individual components of a vector (a_x, say) are real numbers but they are not scalars. Displacement vectors and all vectors derived from displacements automatically satisfy Eq. (1.8). There are, however, other physical quantities which have both magnitude and direction but which are not obviously related to displacements. We need to check carefully to see whether these quantities are vectors.