

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Conjunctive normal form
المؤلف:
J. ELDON WHITESITT
المصدر:
BOOLEAN ALGEBRA AND ITS APPLICATIONS
الجزء والصفحة:
37-40
28-12-2016
3108
There are other normal forms, besides the disjunctive normal form, which are equally useful. One of these represents each function as a product of sums, rather than as a sum of products. If each statement in the preceding section were replaced by its dual, the resulting discussion would be a corresponding treatment of this second form called the conjunctive normal form. To make this clear, the definition and theorems are repeated here in their dual forms. No proofs are needed, of course, because of the principle of duality.
DEFINITION. A Boolean function is said to be in conjunctive normal form in n variables x1, x2, . . . , xn, for n > 0, if the function is a product of factors of the type f1(x1) + f2(x2) + + fn(xn), where fi(xi) is xi or xi' for each i = 1, 2, ... , n, and no two factors are identical. In addition, 0 and 1 are said to be in conjunctive normal form in n variables for n ≥ 0.
THEOREM 1. Every function in a Boolean algebra which contains no constants is equal to a function in conjunctive normal form.
EXAMPLE 1. Write the function (xy' + xz)' + x' in conjunctive normal form.
Solution. The procedure is essentially dual to that of Example 1,in (Disjunctive normal form), although, depending on the initial form of the function, it may require more steps to perform the reduction in one case than in another. Here, after primes are removed from parentheses, the function is factored into linear factors and then extra variables are introduced as needed by adding, within each factor, products of the form ww'. The final step is to expand into linear factors again and remove like factors. The solution for this example is given by the steps below.
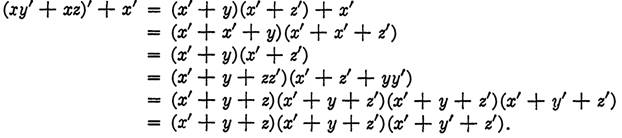
DEFINITION. That conjunctive normal form in n variables which contains 2n factors is called the complete conjunctive normal form in n variables.
THEOREM 2. If each of n variables is assigned the value 0 or 1 in an arbitrary, but fixed, manner, then exactly one factor of the complete conjunctive normal form in the n variables will have the value 0 and all other factors will have the value 1.
Note that to select the factor which will he 0 when a set of values a1, a2, ... , an are assigned to x1, x2, ... , xn in that order, where each ai is 0 or 1, we simply dualize the method of Section (Disjunctive normal form): xi is selected if ai = 0, and x' is selected if ai = 1 for each i = 1, 2, . . . , n. The proper factor is then the sum of these letters, each of which has value 0. All other factors have the value 1.
COROLLARY. Two functions, each expressed in conjunctive normal form in n variables, are equal if and only if they contain identical factors.
EXAMPLE 2. Find and simplify the function f(x, y, z) specified in Table 1-1.
TABLE 1-1
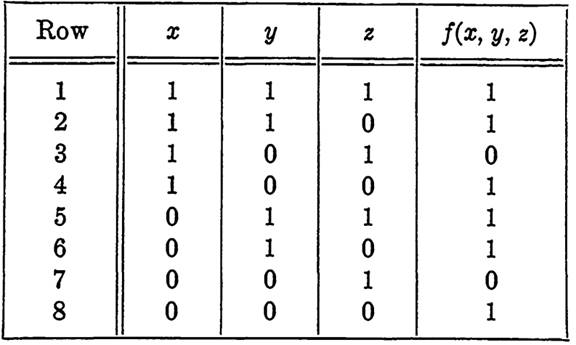
Solution. Since only two rows of the table show the value 0 for the function, it is easiest to use the dual of the method of Example 2, Section (Disjunctive normal form), and write the function first in conjunctive normal form. Selecting factors so that the function will be 0 for the conditions of rows 3 and 7, we have
f(x, y, z) = (x' + y + z) (x + y + z') = y + z'.
In problems of this type, the disjunctive normal form would normally be used if the number of is were less than the number of 0's in the f column, and the conjunctive normal form would be used if the number of 0's were less than the number of 1's.
Again, as in Section (Disjunctive normal form), we can use the conjunctive normal form to find complements of functions written in this form by inspection. The complement of any function written in conjunctive normal form is that function whose factors are exactly those factors of the complete conjunctive normal form which are missing from the given function. For example, the complement of (x + y') (x' + y) is (x + y) (x' + y').
It may be desirable to change a function from one normal form to the other. This can be done more readily than by following the general procedure for converting a function to a particular form. An example will illustrate the method, which is based on the fact that (f')' = f.
EXAMPLE 3. Find the conjunctive normal form for the function
f = xyz + x'yz + xy'z' + x'yz'.
Solution.
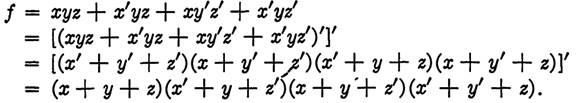
Here the first complement was taken with the aid of DeMorgan's law and the second complement was taken by the method discussed above. These steps could have been reversed, with the same results. A similar procedure will change a function from conjunctive normal form to disjunctive normal form.
REFERENCES
ANDREE, R. V., Selections from Modern Abstract Algebra, Holt, 1958.
BIRKHOFF and 1IAcLANE, A Survey of Modern Algebra, MacMillan, 1948.
HUNTINGTON, E. V., Postulates for the Algebra of Logic, Trans. Am. Math.
Soc. 5 (1904).
JOHNSON, R. E., First Course in Abstract Algebra, Prentice-Hall, 1953.
STABLER, E. R., An Introduction to Mathematical Thought, Addison-Wesley,1953.
STONE, M. H., The Theory of Representations for Boolean Algebras, Trans.
Am. Math. Soc. 40, 37-111 (1936).
 الاكثر قراءة في الجبر البولياني
الاكثر قراءة في الجبر البولياني
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















