The multimode laser. Mode competition and Darwin's survival of the fittest

We consider a laser setup which allows running waves only. This may be achieved by a rectangular arrangement of mirrors where besides the laser-active medium a cell is present which permits the propagation of light in only one direction. The plane waves are represented by

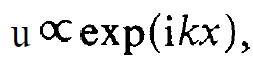         (1.1)

so that

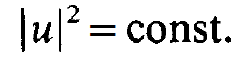       (1.2)

This means that all waves may participate at the atomic emission in the same way, at least as far as their spatial behavior is concerned. Thus the transition rate W_λμ (with 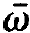_μ = 6) simplifies as follows:

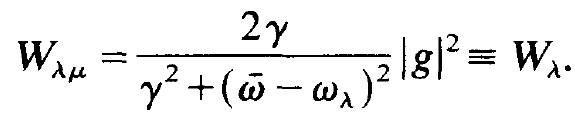    (1.3)

We are treating a homogeneously broadened atomic line. A closer inspection shows that we may pull the expressions W_λ in front of the sums over μ occurring. This means that the photon annihilation and production rate is determined by the total inversion

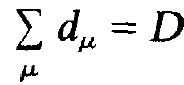 (1.4)

only. In order to derive an equation for this D we over μ. Therefore we need only to take into account the ensemble of atoms but no more their individual occupation numbers. When we confine our analysis to the stationary state we may put n, = 0 and D = 0. We thus obtain the equations

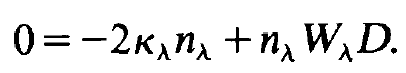 (1.5)

Because we may write (1.5) also in the form

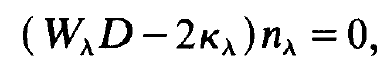     (1.6)

this set of equations means that either the photon number n, or its factor vanish,

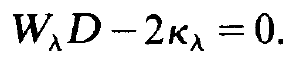    (1.7)

Let us assume that for a set of certain modes n, ≠ 0. For these modes which we may numerate λ = l , 2 , . . . , eq. (1.7) must hold. But this implies

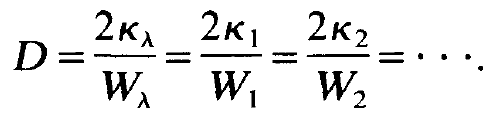   (1.8)

Because the inversion D is uniquely determined, the right hand sides must be equal to each other. Let us consider the following situation. All modes have the same lifetime but they are situated at different frequencies. For different frequencies the corresponding W's differ from each other. Under this hypothesis the expressions 2k_λ /W_λ, A = 1, 2, . . . must be different from each other. Thus we have found a contradiction which stems from the fact that we have assumed a set of modes with non-vanishing photon numbers n,. This contradiction can be solved only, if at most only a single n, differs from 0, whereas all other n, vanish. As one can easily convince oneself that n, is different from 0 whose frequency lies closest to the atomic transition frequency. Of course, our considerations can be immediately generalized to the case where a discrimination of the modes is caused by their different lifetimes in the laser resonator. These considerations give rise to the important result that in a laser only one mode is selected if the frequency distribution of the modes and their lifetimes are taken into account. In other words, in the sense of biological selection only one mode can win mode competition and all others have to die out. This is a precise mathematical formulation of Darwin's survival of the fittest. If we visualize the excited atoms as food which is continuously fed into the system and the photons as animals the result has the following meaning: One kind of animal has a better access to the food. It grows more quickly and this kind of animal can eat more food. The other animals cannot compete in eating and eventually perish. As this example shows, coexistence of animals can be reached if they are enabled to live from separated resources of food so that the animals eating fastest cannot take away the food of the other animals. In biology this is achieved by ecological niches. In the laser, in an abstract sense, a similar situation can be achieved by letting different kinds of atoms generate different kinds of photons. This may happen, for example, in the following cases:

(1) The atomic line is inhomogeneously broadened.

Let us consider the special case in which only two kinds of atoms with different optical transition frequencies 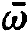₁, and  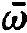 ₂ are present whereby the corresponding emission lines do not overlap. In such a case the photons belonging to the modes with frequencies ⍵₁= 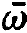₁ and ⍵₂= ₂, are separately supported and can coexist. The general case of continuously distributed central frequencies (inhomogeneously broadened line).

(2) The modes are standing waves.

We find a similar situation if the modes are standing waves and the line is for instance homogeneously broadened. We explain this situation by means of the example of two modes whose spatial distribution is presented in fig. 1.1. If only mode 2 is present it generates an inversion by spatial hole burning as presented in fig. 1.2. Evidently mode 1 experiences an

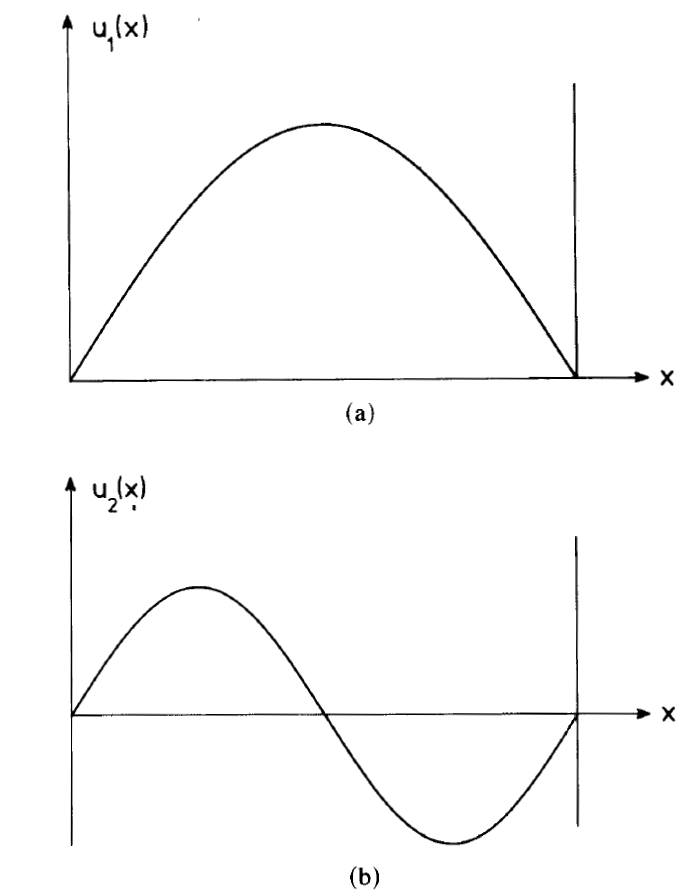
Fig. 1.1. In order to illustrate the possibility of coexistence of standing waves, in (a) and (b) the limiting cases of the two longest wave-lengths are shown. The mode amplitude is plotted versus the spatial coordinate x in axial direction.

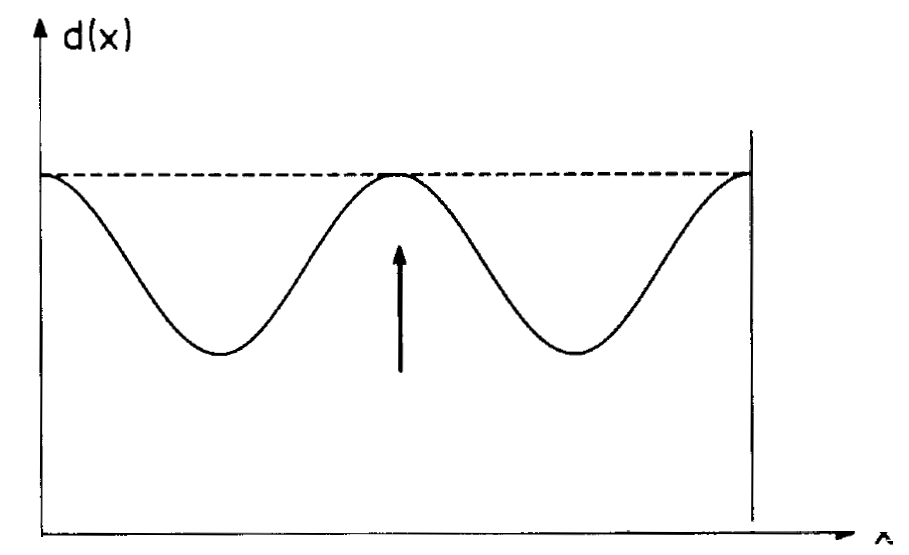
Fig. 1.2. In this figure that inversion is plotted against x which results from the presence of mode 2 alone.

unsaturated inversion there where the mode 1 itself has its maximum (fig. 1.2). Thus mode 1 can live on that part of the unsaturated inversion. Quite evidently both modes are at least partly supported by two different kinds of atoms which are located at different positions. Thus these modes can coexist provided the unsaturated inversion d₀ is big enough. On account of the figures it might seem as if this effect is important only for large wavelengths. But one may show that this effect is independent of the mode wave-lengths in the resonator. In this way also several modes can coexist. In the next section we want to prove this rigorously.