Relaxation oscillations

In this section we wish to further study the time dependent processes in the single mode laser. But we shall no more assume that the inversion follows the photon number instantaneously. While this assumption is well justified if the photon numbers are small this is no more the case for higher photon numbers. Instead we consider small deviations of n and the occupation numbers from their corresponding stationary values. To this end we assume that n or N, initially deviate from their stationary states a little. We wish to show that n and N_j perform damped oscillations or, in other words, relaxation oscillations. Let us consider as an example a 3-level laser in which the optical transition occurs between the two upper levels. The corresponding occupation numbers are again denoted by N₁ and N₂. Let us assume that the lower transition from level 1 to level 0 takes place very rapidly (compare also the exercise at the end of this section). In this case the laser equations read as follows: Equation for the photons

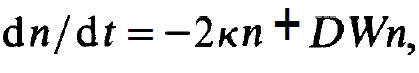   (1.1)

where D= N₂- N₁.

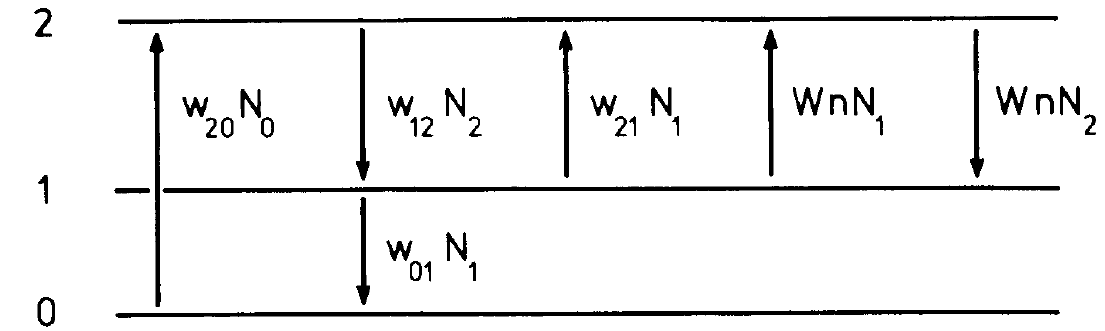
Fig. 1.1. Transition scheme in a system of three-level atoms in which the optical transition takes place from the uppermost to the middle level.

Equation for the occupation numbers

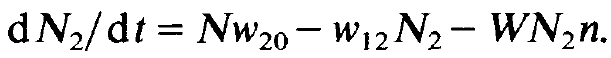  (1.2)

N is the total number of atoms. Because of our assumption that the lower laser level is practically unoccupied we may replace D by N₂ in the equation for the photons. We now assume that deviations of n and N₂ from their stationary states N­₀ and N⁰₂, respectively, have occurred. We study whether and in which way a stationary state will be reached again. To this end we make the hypothesis

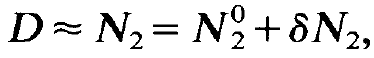 (1.3)

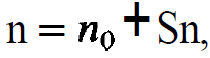   (1.4)

where the stationary solutions n₀ and N⁰₂ are fixed by the conditions

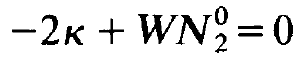   (1.5)

and

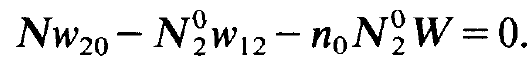    (1.6)

Inserting (1.3) and (1.4) in (1.1) and (1.2) we obtain terms which contain only the stationary solution, terms proportional to δn or δN₂ and finally expressions which contain the product Sn δN₂. We assume that the deviations from the equilibrium values are only small. This allows us to neglect the term Sn δN₂ being of higher order. Because the stationary solution obeys the eqs. (1.5) and (1.6), this solution drops out and we only retain the equations

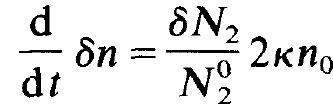     (1.7)

and

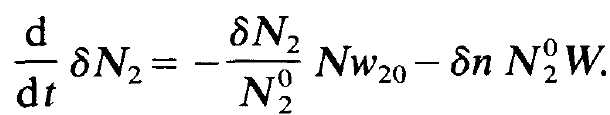   (1.8)

These are two coupled linear differential equations which we can solve as usual by the exponential ansatz

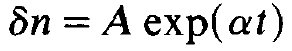   (1.9)

and

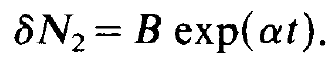    (1.10)

We insert (1.9) and (1.10) in (1.7) and (1.8), perform the differentiation with respect to time, and divide the resulting equations by the exponential function. We then obtain the following two equations

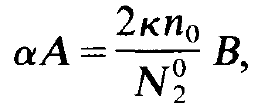    (1.11)

and

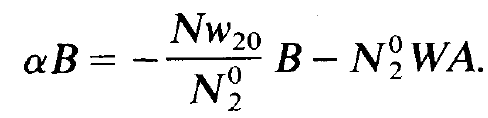    (1.12)

These are homogeneous equations for the unknowns A and B. According to elementary theorems of algebra a non-trivial solution is possible only if the corresponding determinant

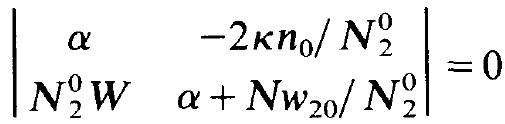    (1.13)

vanishes. This determinant can be easily evaluated. Inserting the values for N⁰₂ and n₀ according to (1.5) and (1.6) we obtain an equation for a:

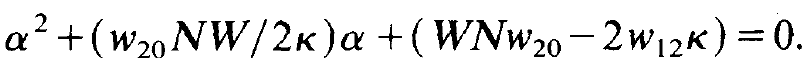    (1.14)

We represent the solution of this quadratic equation in the form

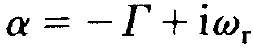   (1.15)

where Γ is given by

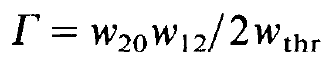   (1.16)

and w_r by

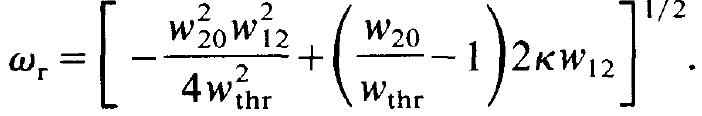    (1.17)

We have assumed that the second term in the bracket in (1.17) is bigger than the first term, so that w_r is a real frequency. Furthermore we have used the abbreviation

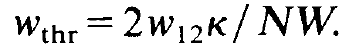   (1.18)

The index "thr" is an abbreviation of "threshold". The most general solution for the photon number may be represented in the form

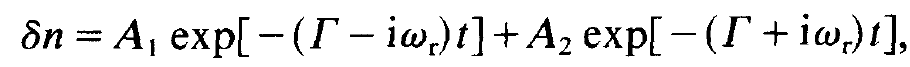   (1.19)

where A₁ and A₂ are fixed by the initial conditions for the photon number n and the occupation number N₂. Obviously the system relaxes towards the stationary state while it performs oscillations (fig. 1.2).

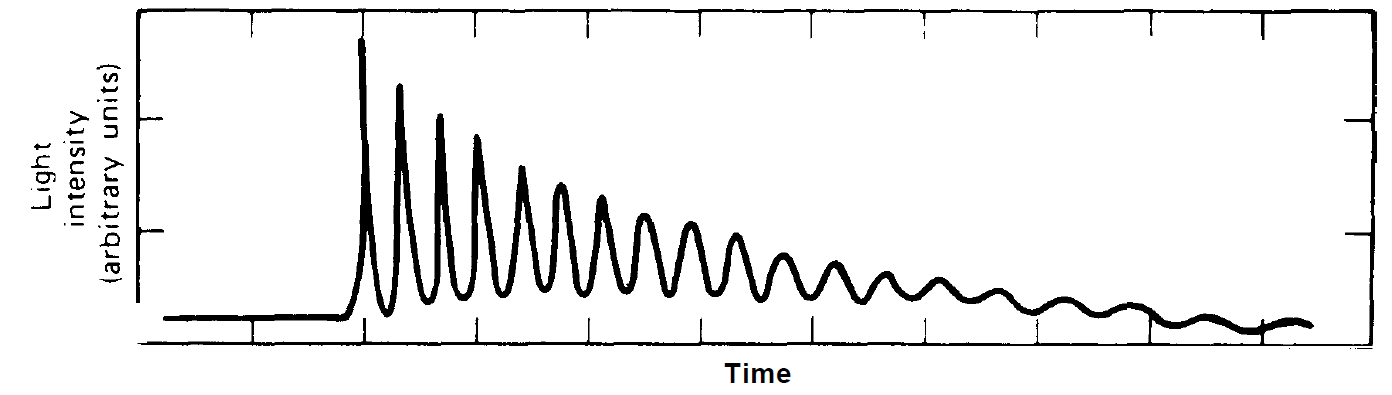
Fig. 1.2. Example of relaxation oscillations.