In Chapter of(Basic Properties of Functions on R¹), we discussed the elementary properties of functions defined on R¹ with range in R¹. We were also concerned with functions whose domain consisted of a part of R¹, usually an interval. In this section we develop properties of functions with domain all or part of an arbitrary metric space S and with range in R¹. That is, we consider real valued functions. We first take up the fundamental notions of limits and continuity. 

Definition

Suppose that f is a function with domain A, a subset of a metric space S, and with range in R¹; we write f : A → R¹. We say that f(p) tends to J asP tends toP₀ through points of A if (i) p₀ is a limit point of A, and (ii) for each ε> 0 there is a δ> 0 such that

                                                     |f(p) − l| <ε for all p  in A

                        with the property that 0 <d(p,p₀)<δ. We write

                                                         f(p) → l as p → p₀,p ∈ A.

We shall also use the notation

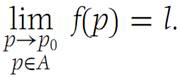
      Observe that the above definition does not require f(p₀) to be defined, nor does p₀ have to belong to the set A. However,          when both of these conditions hold, we are able to define continuity for real-valued functions.

        Definitions

Let A be a subset of a metric space S, and suppose f : A → R¹ is given. Let p₀ ∈ A. We say that f is continuous with respect to A at p₀ if (i) f(p₀) is defined, and (ii) either p₀ is an isolated point of A or p₀ is a limit point of A and

                                            f(p) → f(p₀) as p → p₀,p ∈ A.

We say that f is continuous on A if f is continuous with respect to A at every point of A. If the domain of f is the entire metric space S, then we say that f is continuous at p₀, omitting the phrase “with respect to A.” The definitions of limit and continuity for functions with domain in one metric space S₁ and range in another metric space S₂ are extensions of those given above. The basic properties of functions defined on R¹ discussed do not always have direct analogues for functions defined on a subset of a metric space. For example, the Intermediate-value theorem ( (Intermediate-value theorem) Suppose f is continuous on [a,b], c ∈ R¹, f(a)<c, and f(b)>c. Then there is at least one number x₀ on [a,b] such that f(x₀) = c.)) for functions defined on an interval of R¹ does not carry over to real-valued functions defined on all or part of a metric space. However, when the domain of a real-valued function is a compact subset of a metric space,  For example, the following theorem is the analogue of the boundedness theorem ( (Boundedness Theorem) Suppose that the domain of f is the closed interval I ={x:a ≤ x ≤ b}, and f is continuous on I. Then the range of f is bounded.).

Theorem 1.1

Let A be a compact subset of a metric space S. Suppose that f :A → R¹ is continuous on A. Then the range of f is bounded.

Proof

We assume that the range is unbounded and reach a contradiction. Suppose that for each positive integer n, there is a p_n ∈ A such that |f(p_n)| >n. Since A is compact, the sequence {p_n}⊂ A must have a convergent subsequence, say {q_n}, and q_n → p¯  with  p¯ ∈ A. Since f is Continuous on A, we have f(q_n) → f(p¯) as n →∞. Choosing ε = 1in the definition of continuity on A and observing that d(q_n, p¯) → 0as n →∞, we can state that there is an N1 such that for n>N₁, we have

                                                |f(q_n) − f(p ¯)| < 1    whenever  n>N₁.

We choose N₁ so large that |f(p ¯)| <N₁. Now for n>N₁ we may write

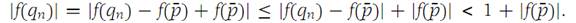
Since q_n is at least the nth member of the sequence {p_n}, it follows that |f(q_n)| >n for each n. Therefore,

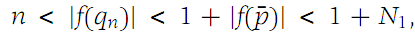
a contradiction for n sufficiently large. Hence the range of f is bounded.

Note the similarity of the above proof to that of (Boundedness Theorem). Also, observe the essentialmanner in which the compactness of A isemployed. The result clearly does not hold if A is not compact.

Problems

In the following problems a set A in ametric space S is given. All functions are real-valued (range in R¹) and have domain A.

1. If c is a number and f(p)= c for all p ∈ A, then show that for any limit point p₀ of A, we have

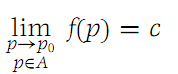
           (theorem on limit of a constant).

      Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(122-124)

اخر الاخبار

اخبار العتبة العباسية المقدسة

عباس.. طفل فقد والده فوجد في خدمة زائري عاشوراء وطنًا آمنًا

شعبة الخطابة النسوية تواصل إقامة مجالس العزاء في شهر المحرم الحرام

لليوم الخامس.. العتبة العباسية المقدسة تقيم مجلس عزاء في صحن مرقد أبي الفضل العباس (عليه السلام)

قسم الشؤون الفكرية يقيم مجلس عزاء حسيني في العاصمة التنزانية دار السلام

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد

مواضيع ذات صلة

Elementary Theory of Metric Spaces-The Schwarz and Triangle Inequalities; Metric Spaces

Elementary Theory of integration -The Darboux Integral for Functions on RN

Elementary Theory of integration -The Logarithm and Exponential Functions

Elementary Theory of integration -The Riemann Integral

Differentiation and Integration in RN-The Riemann Integral in RN

Differentiation and Integration in RN-The Darboux Integral in RN

Differentiation and Integration in RN-The Derivative in RN

Differentiation and Integration in RN-Taylor,s Theorem; Maxima and Minima

Differentiation and Integration in RN-Partial Derivatives and the Chain Rule

Continuity

Basic Properties of Functions on R1 -The Heine–Borel Theorem

Basic Properties of Functions on R1 -The Cauchy Criterion