In addition to the development of the integral by the method of Darboux, there is a technique due to Riemann that starts with a direct approximation of the integral by a sum. The main result of this section shows that the two definitions of integral are equivalent.

Definitions

Suppose that Δ is a subdivision of I ={x : a ≤ x ≤ b} with subintervals I₁,I₂,...,I_n. We call the mesh of the subdivision Δ the length of the largest subinterval among l(I₁), l(I₂),...,l(I_n). The mesh is denoted by Δ. Suppose that f is defined on I and that Δ is a subdivision. In each subinterval of Δ we choose a point x_i ∈ I_i . The quantity

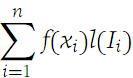
Is called a Riemann sum.

For nonnegative functions it is intuitively clear that a Riemann sum with very small mesh gives a good approximation to the area under the curve. (See Figure 1.1.)

Definitions

Suppose that f is defined on I ={x : a ≤ x ≤ b}. Then f is Riemann integrable on I if there is a number A with the following property: For every Ԑ> 0 there is a δ> 0 such that for every subdivision Δ with mesh smaller than δ, the inequality(1.1)

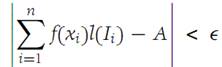
holds for every possible choice of xi in Ii . The quantity A is called the Riemann integral of  f .

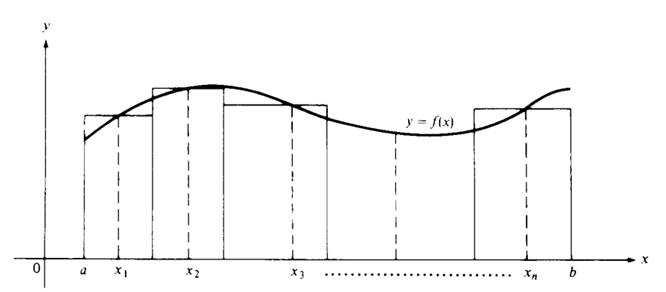
Figure 1.1 A Riemann sum.

Theorem 1.1

If f is Riemann integrable on I ={x:a ≤ x ≤ b}, then f is bounded on I.

Proof

In the definition of Riemann integral, choose Ԑ = 1 and let  Δ  be a subdivision such that inequality (1.1) holds. We have

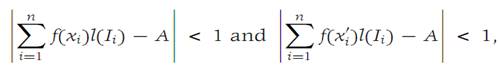
where x₁,x₂,...,x_n and x^/₁,x^/₂,...,x^/_n are any points of I such that x_i and x^/_iare in I_i . Therefore,

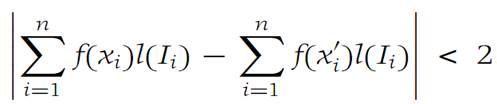
Now select x_i =x^/_i for i = 2, 3,...,n. Then the above inequality becomes

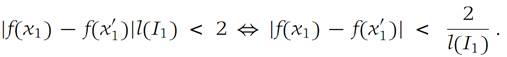
Using the general inequality |α|−|β| < |α − β|, we obtain

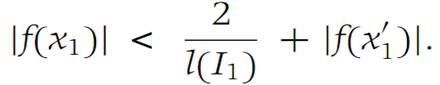
Fix x^/₁ and observe that the above inequality is valid for every x₁ ∈ I₁.

Hence f is bounded on I₁. Now the same argument can be made for I₂,I₃,...,I_n. Therefore, f is bounded on I.

Theorem 1.2

If f is Riemann integrable on I ={x: a ≤ x ≤ b}, then f is Darboux  integrable

on I. Letting A denote the Riemann integral, we have

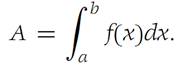
Proof

In Formula (1.1), we may replace Ԑby Ԑ/4 for a subdivision Δ with sufficiently small mesh: 1).2)

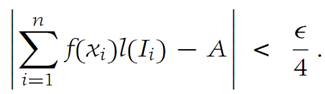
Let M_i and mi denote the least upper bound and greatest lower bound, respectively, of  f in I_i . Then there are points x^/_iand x^//_I such that

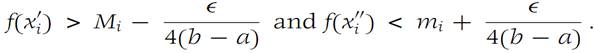
These inequalities result just from the definition of l.u.b. and g.l.b. Then we have

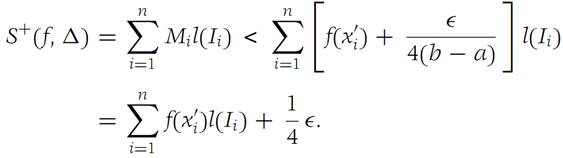
Hence, using inequality (1.2), we obtain(1.3)

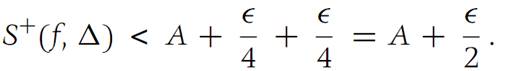
Similarly,

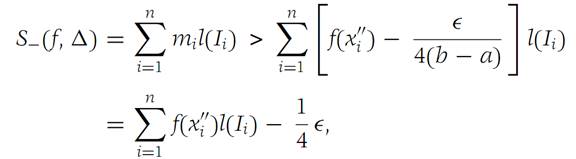
And(1.4)

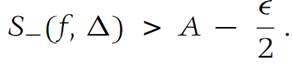
Subtraction of inequality (1.4) from inequality (1.5) yields

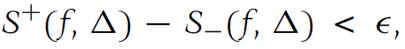
thus f is Darboux  integrable. Furthermore, these inequalities show that

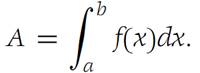
We omit the proof of the theorem that shows that every Darboux integrable function is Riemann integrable. Thus we state the following result:

Theorem 1.3

A function f is Riemann integrable on [a,b] if and only if it is Darboux integrable on [a,b].

In light of Theorem 1.2 we shall now drop the terms Darboux and Riemann, and just refer to functions as integrable.

One of the most useful methods for performing integrations when the integrand is not in standard form is the method known as substitution. For example, we may sometimes be able to show that a complicated integral has the form

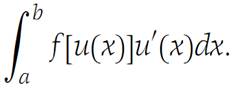
Then, if we set u = u(x), du = u^/(x)dx, the above integral becomes

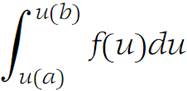
and this integral may be one we recognize as a standard integration. In an elementary course in calculus these substitutions are usually made without concern for their validity. The theoretical foundation for such processes is based on the next result.

Theorem 1.4

Suppose that f is continuous on an open interval I. Let u and u^/be continuous on an open interval J , and assume that the range of u is contained in I. If a,b ∈ J , then(1.6)

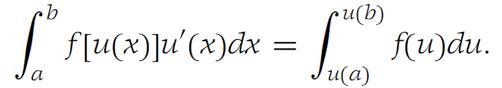
Proof

Let c ∈ I and define(1.7)

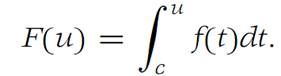
From the Fundamental theorem of calculus(Theorem (Fundamental theorem of calculus—first form)) we have

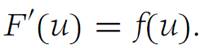
Defining G(x) = F[u(x)], we employ the Chain rule to obtain

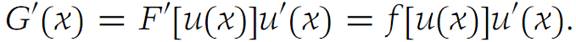
Since all functions under consideration are continuous, it follows that

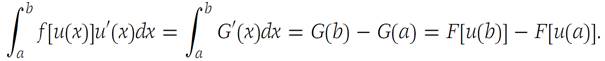
From equation (1.7) above, we see that

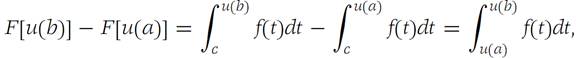
and the theorem isproved.

Problems

1. (a) Suppose that F is continuous on I ={x : a ≤ x ≤ b}. Show that all upper and lower Darboux sums are Riemann sums.

(b) Suppose that f is increasing on I ={x : a ≤ x ≤ b}. Show that all upper and lower Darboux sums are Riemann sums.

(c) Give an example of a bounded function f defined on I in which a Darboux sum is not a Riemann sum.

2. Suppose that u, u^/, v, and v^/are continuous on I ={x : a ≤ x ≤ b}. Establish the formula for integration by parts:

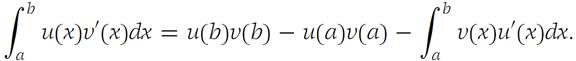
3. State conditions on u, v, and f such that the following formula is valid:

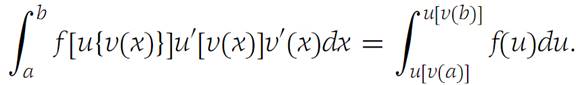
Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(91-96)