
Continuity
 المؤلف:
Murray H. Protter
المؤلف:
Murray H. Protter
 المصدر:
Basic Elements of Real Analysis
المصدر:
Basic Elements of Real Analysis
 الجزء والصفحة:
21-27
الجزء والصفحة:
21-27
 24-11-2016
24-11-2016
 1113
1113
Most of the functions we study in elementary calculus are described by formulas. These functions almost always possess derivatives. In fact, a portion of any first course in calculus is devoted to the development of routine methods for computing derivatives. However, not all functions possess derivatives everywhere. For example, the functions (1 + x2)/x, cot x, and sin(1/x) do not possess derivatives at x =0 no matter how they are defined at x =0.
As we progress in the study of analysis, it is important to enlarge substantially the class of functions we examine. Functions that possess derivatives everywhere form a rather restricted class; extending this class to functions that are differentiable except at a few isolated points does not enlarge it greatly. We wish to investigate significantly larger classes of functions, and to do so we introduce the notion of a continuous function.
Definitions
Suppose that f is a function from a domain D in R1 to R1. The function f is continuous at a if (i) the point a is in an open interval I contained in D, and (ii) for each positive number ε there is a positive number δ such that
|f(x) − f(a)| <ε whenever |x − a| <δ.
If f is continuous at each point of a set S, we say that f is continuous on S. A function f is called continuous if it is continuous at every point of its domain. The geometric significance of continuity at a point a is indicated in Figure 1.1. We recall that the inequality |f(x) − f(a)| <ε is equivalent to the double inequality
−ε<f(x) − f(a) < ε,
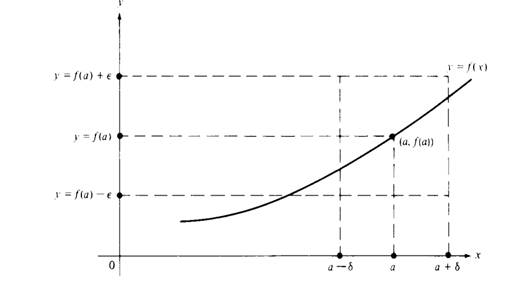
Figure 1.1 The graph of f is in the rectangle for a − δ<x<a + δ.
Or
f(a) − ε<f(x)<f(a) + ε.
Similarly, the inequality |x − a| <δ is equivalent to the two inequalities
a − δ<x<a + δ.
We construct the four lines x a − δ, x a + δ, y f(a) − ε, and y =f(a) + ε, as shown in Figure 1.1. The rectangle determined by these four lineshasitscenter at the point with coordinates (a, f(a)). The geometric interpretation of continuity at a point may be given in terms of this rectangle. A function f is continuous at a if for each ε> 0 there is a number δ> 0 such that the graph of f remains within the rectangle for all x in the interval (a − δ, a + δ).
It is usually very difficult to verify continuity directly from the definition. Such verification requires that for every positive number ε we exhibit a number δ and show that the graph of f lies in the appropriate rectangle.
However, if the function f is given by a sufficiently simple expression, it is sometimes possible to obtain an explicit value for the quantity δ corresponding to a given number ε. We describe the method by means of two examples.
Example 1
Given the function
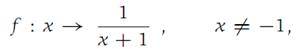
and a = 1, ε = 0.1, find a number δ such that |f(x) − f(1)| < 0.1 for |x − 1| <δ.
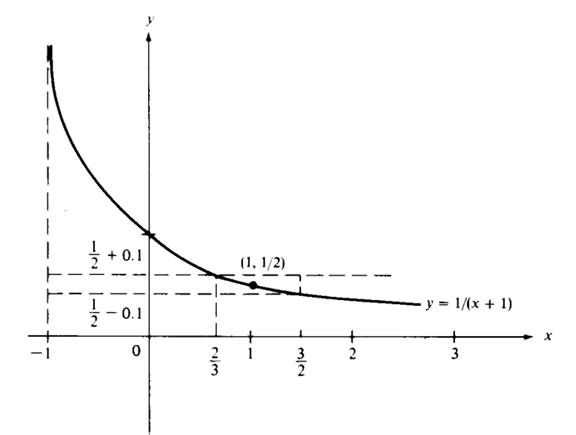
Figure 1.2
Solution. We sketch the graph of f and observe that f is decreasing for x> −1 (see Figure 1.2). The equations f(x)−f(1) = 0.1, f(x)−f(1) =−0.1 can be solved for x. We find
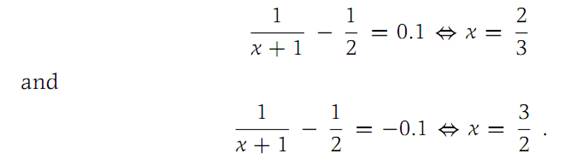

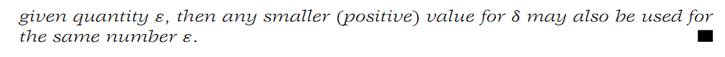
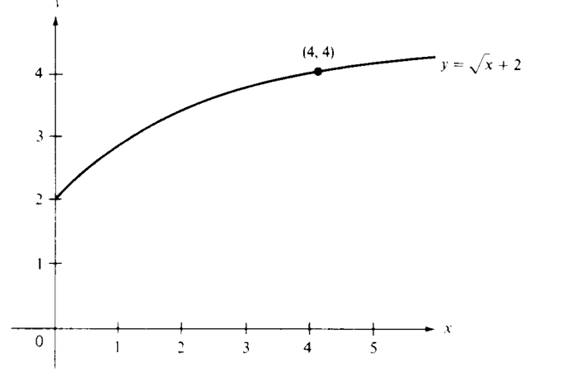
Figure 1.3
Example 2
Consider the function
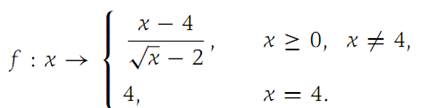
If ε = 0.01, find a δ such that |f(x) − f(4)| < 0.01 for all x such that |x − 4| <δ.
Solution.
If x ≠ 4, then factoring x − 4, we get
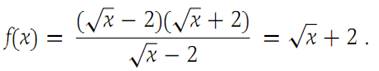
The graph of f is shown in Figure 1.3, and we observe that f is an increasing function. We solve the equations f(x) − f(4) =0.01 and f(x) − f(4) =−0.01 and obtain
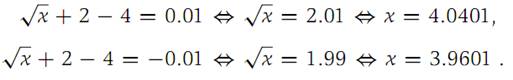
Since f is increasing, it follows that |f(x) − f(4)| < 0.01 for 3.9601 <x< 4.0401. Selecting δ = 0.0399,
we find that |f(x) − f(4)| <ε for |x − 4| <δ.
Definition
Suppose that a and L are real numbers and f is a function from a domain D in R1 to R1. The number a may or may not be in the domain of f . The function f tends to L as a limit as x tends to a if (i) there is an open interval I containing a that, except possibly for the point a, is contained in D, and (ii) for each positive number ε there is a positive number δ such that
|f(x) − L| <ε whenever 0 < |x − a| <δ.
If f tends to L as x tends to a, we write
f(x) → L as x → a
and denote the number L by
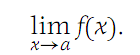
(i) We see that a function f is continuous at a if and only if a is in the domain of f and f(x) → f(a) as x → a.
(ii) The condition 0 < |x − a| <δ (excluding the possibility x= a)is used rather than the condition |x−a| <δ as in the definition of continuity, since f may not be defined at a itself.
Problems
In Problems1 through 8 the functions are continuous at the value a given. In each case find a value δ corresponding to the given value of ε such that the definition of continuity is satisfied. Draw a graph.
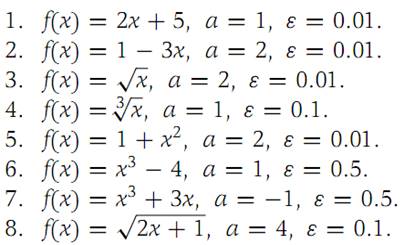
Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 Page(21-27)
 الاكثر قراءة في التحليل الحقيقي
الاكثر قراءة في التحليل الحقيقي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


