Orbiting Bodies

When a body such as a planet orbits around a more massive body such as the Sun, the orbit does not close on itself, as expected from Newton’s universal law of gravitation and Kepler’s laws. The general theory of relativity (GTR) calculates the correct value for this precession of the orbital ellipse, determining that its complicated equations reduce to an equation similar in form to that of the classical Kepler problem, with an additional quadratic term that causes the precession. Can you provide a conceptual argument in GTR for the precession of the ellipse?

Answer

The general theory of relativity (GTR) in the Schwarzschild metric approximation for the space-time metric about the Sun predicts a precession of the planetary orbit. Mercury, for example, accumulates a total GTR precession of about 43 seconds of arc per Earth century. There are many other precessional effects acting on the orbit, including effects from all the other planets orbiting the Sun, all these perturbations amounting to a whopping 532 seconds of arc per century, all but the residual 43 seconds being explained with Newtonian mechanics.

When the angular change around the orbit is calculated with GTR in the φ-coordinate and then independently in the r-coordinate, there is disagreement, which is the conceptual source of the effect. Or one can assign an additional equivalent mass distribution for the energy in the gravitational field surrounding the Sun, creating a metric that does not correspond to a 1/r potential, perhaps 1/r² or 1/r³, or some other function of r instead of the Newtonian inverse r potential. All these functions of r will exhibit a precession of the orbit.

In addition, a body in orbit such as a planet orbiting the Sun actually does not obey Kepler’s third law precisely. That is, even when we ignore the precession of the orbit by assuming its return to the same angle with respect to the stars, the period of orbit needs correction. This period of orbit correction is a so-called fourth independent general test of the GTR, in addition to the gravitational redshift, the deflection of starlight, and the precession of an orbit.

The correction to the period of orbit, as calculated by Preston and Weber in the reference below, begins by putting the reference clock at the center of the orbit. The classical Newtonian period of orbit is given by Kepler’s third law: 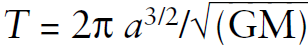 , where a is the semimajor axis of the ellipse and M is the mass value of the central body. For the elliptical orbit of eccentricity ε, in the GTR one can calculate the period of orbit in the radial coordinate T_r = T (1/α + 3/2 r_g/r) and in the φ-coordinate T_φ = T (1/α – 3/2 (r_g/r) (ε²/α)), where α = (1 – ε²)^3/2. For orbiting bodies near potential black holes, this correction can get large as the radial distance r approaches the Schwarzschild radius r_g = 2GM/c².