Quantized Hall Effect

The Hall effect was discovered by Edwin Hall in 1879. “. . . A charged particle moving in a magnetic field feels a ‘Lorentz’ force perpendicular to its direction of motion and the magnetic field. As a direct consequence of this Lorentz force, charged particles will accumulate to one side of a wire if you send current through it and hold it still in a [perpendicular] magnetic field. . . .” When the transverse voltage is measured at a fixed current, the Hall resistance is measured and increases linearly with an applied magnetic field.

The conduction electrons in a solid behave like a gas of electrons. So the discovery of the quantized Hall effect in 1980 by von Klitzing and his research group when he was investigating the conductance properties of two-dimensional electron gases at very low temperatures and high magnetic fields was a surprise. What is the physics behind this quantized Hall effect?

Answer

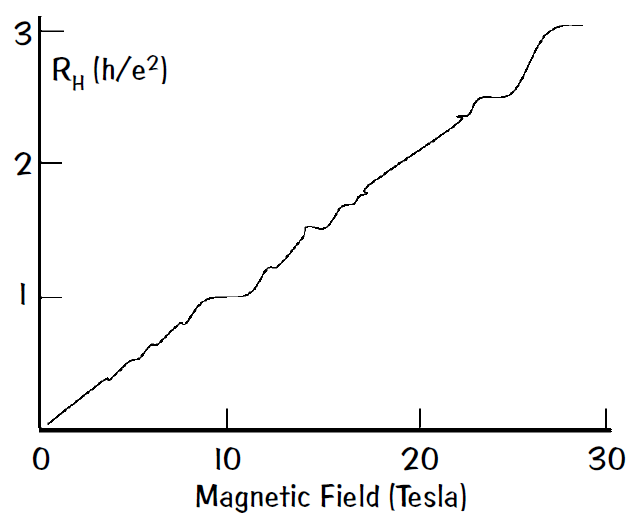
In a two-dimensional metal or semiconductor, the standard Hall effect is observed, but at low temperatures, a series of steps appear in the Hall resistance as a function of magnetic field instead of showing the typical monotonic increase. By confining the electron system in the third dimension to confine the electron gas to two dimensions, only specific electron wave functions meet the boundary conditions, so only certain quantized energy levels are available for the electrons. These steps in the Hall resistance occur at incredibly precise values of resistance, which are the same no matter what sample is investigated that is, the resistance is quantized in units of h/e² divided by an integer. This amazing result is the quantized Hall effect.

Recall that electrons have a spin 1/2 and obey the Pauli exclusion principle. As electrons are added to an energy band, they fill the available energy band states, just as water fills a bucket. The states with the lowest energy are filled first, followed by the next higher ones. At absolute zero temperature T = 0 K, the energy levels are all filled up to a maximum energy called the Fermi level. At higher temperatures one finds that the transition region between completely filled states and completely empty states is gradual rather than abrupt and described by the Fermi function, which has a value of 1 for energies that are more than a few times kT below the Fermi energy, equals 1/2 if the energy equals the Fermi energy, and decreases exponentially for energies that are a few times kT larger than the Fermi energy.

Consider the ideal case of a fixed Fermi energy and a changing applied magnetic field. In the presence of the magnetic field, the density of electron energy states in 2-D is no longer constant as a function of energy and bunches into discrete energy levels, called Landau levels, of finite width separated by the cyclotron energy, with energy regions between the Landau levels where there are no allowed electron states. As the magnetic field is swept to higher values, the Landau levels move relative to the Fermi energy.

When the Fermi energy lies in a gap between Landau levels, there are no available states to scatter into, so there is no scattering, and the electrical resistance falls to zero. The Hall resistance for the Hall current cannot change from the quantized value whenever the Fermi energy is in a gap between Landau levels, so one measures a plateau. Only when the Fermi energy is in the Landau level can the Hall voltage change and a finite resistance value appear.