حياته :

لم يصلنا سوى القليل عن اخبار الخوارزمي، وما نعرفه عن اثاره اكثر واهم مما نعرفه عن حياته الخاصة، وهو محمد بن موسى الخوارزمي، اصله من خوارزم، ونجهل تاريخ مولده، غير انه عاصر المأمون، اقام في بغداد حيث ذاع اسمه وانتشر صيته بعدما برز في الفلك والرياضيات، اتصل بالخلفية المأمون الذي اكرمه، وانتمى الى بيت الحكمة واصبح من العلماء الموثوق بهم، وقد توفي بعد عام 232هـ :

آثاره :

• ترك الخوارزمي عددا من المؤلفات اهمها :
• الزيج الاول.
• الزيج الثاني المعروف بالسند هند.
• كتاب الرخامة.
• كتاب العمل بالاسطرلاب.
• كتاب الجبر والمقابلة.

ومما يتماز به انه اول من فصل بين علمي الحساب ARITHMETIQUE والجبر ALGEBRE، كما انه اول من عالج علم الجبر بأسلوب منطقي علمي، فنقله من حالته البدائية الى مستوى راق افاق منه علماء الغرب في بحوثهم الرياضية، اما لفظة جبر فهي من وضع الخوارزمي، وهي تدل على العلم المعروف اليوم بهذا الاسم ALGEBRE.

كتاب الجبر والمقابلة :

كلف المأمون الخوارزمي بوضع كتاب الجبر والمقابلة ليفيد منه الناس في التجارة، وقياس مساحة الارض، وتوزيع الارث على المستحقين، وتوزيع الانصبة على الموصى لهم، قال الخوارزمي في مقدمة الكتاب : وقد شجعنا ما فضل الله به الامام (المامون) امير المؤمنين مع الخلافة التي حاز له ارثها، واكرمه بلباسها، وحلاه بزينتها، من الغربة في الادب، وتقريب اهله وادناهم وبسط كنفه لهم، ومعونته اياهم على ايضاح ما كان مستبهماً، وتسهيل ما كان مستوعراً، على اني الفت من كتاب الجبر والمقابلة كتابا مختصرا، حاصرا للطيف الحساب وجليلة، لما يلزم الناس من الحاجة اليه في مواريثهم ووصاياهم، وفي مقاسمتهم واحكامهم وتجارتهم، وفي جميع ما يتعاملون به بينهم من مساحة الأرضين وكري الانهار والهندسة، وغير  ذلك من وجوهه وفنونه .. وبالله توفيقي في هذا وفي غيره، وعليه توكلت، وهو رب العرش العظيم.

ولفهم اعمال الجبر عند الخوارزمي ينبغي ان نقف على الاصطلاحات التي وضعها لهذا العلم :

• الجذر وهو المعروف في الجبر الحديث باسم المجهول : س، وكان علماء الجبر يسمونه الشيء.
• المال هو الجبر مضروبا بنفسه، أي مربع الجذر : س2.
• المفرد هو العدد الخالي من الجذر، أي من المجهول : 5.4.5...إلخ.
• جزء الشيء هو معكوس الشيء، أي معكوس الجذر : س/1

والخوارزمي لم يذكر سوى ستة انواع من المعادلات EQUATIONS هي  :

• الاموال التي تعادل الجذور : م س2 = ب س
• الاموال الي تعادل عدداً : م س2 = ح.
• الجذور التي تعادل : ب س = ح.
• الاموال والجذور التي تعادل عددا : م س2 + ب س = ح.
• الجذور والاعداد التي تعادل اموالا : ب س + ح = م س2.
• الاموال والاعداد التي تعادل جذوراً : م س2 + ح = ب س.

اما حل هذه المعادلات فكان يقوم به الخوارزمي بواسطة احدى طريقتين، الطريقة الخالية من الرموز، أي من الاصطلاحات الجبرية التي ارودناها، والطريقة التي تستخدم هذه الرموز، ولنضرب مثلين على هاتين الطريقتين اخذناهما من كتاب الجبر والمقابلة.

حل معادلة من دون رموز :

قال الخوارزمي : مالان وعشرة اجذار تعادل ثمانية واربعين درهما، والمطلوب ايجاد مقدار المال وهذا هو الحل الذي وضعه : ومعناه أي مالين اذا جمعا وزيدا عليهم مثل عشرة اجذار احدهما بلغ ثمانية واربعين درهما، فينبغي ان ترد المالين الى مال واحد، وقد علمت ان مالا من مالين نصفهما، فاردد كل شيء في المسالة الى نصفه فكانه : مال وخمسة اجذار يعدل 24 درهما، ومعناه أي مال اذا زدت عليه خمسة اجذار بلغ اربعة وعشرين؛ ننصف الاجذار فتكون اثنين ونصفاً، فاضربهما في مثلها فتكون ستة وربعا، فزدها على الاربعة والعشرين فيكون ثلاثين درهما وربع الدرهم، فخذ جذرها وهو خمسة وصنف فانقص منها نصف الاجذار وهو اثنان ونصف يبقى ثلاثة وهو جذر المال، والمال تسعة.

حل معادلة بواسطة رموز :

وضع الخوارزمي حل معادلة بواسطة الرموز على الوجه التالي :

2س² + 10س = 48.

س² + 5س = 24.

ولما كان الخوارزمي اول من الف في الجبر من رياضيي العرب، فان الجبر العربي توصل، على يده، الى حل المعادلات من الدرجة الثانية واستخرج قيمة جذورها الموجبة POSTTIVES، كما توصل الى معرفة لمعادلات ذات الجذور التخيلية IMAGINAIRES RACINES وهي التي تكون فيها الكمية الواقعة ما تحت علامة الجذر سلبية، والتي يعبر عنها الجبر بـ 0 > أو 0 > ت4ac – b².

وقد يكون رياضيو الاغريق قد توصلوا الى هذه النتائج، وقد يكون الخوارزمي اطلع على ما توصلوا اليه، غير ان معلوماتهم كانت مبعثرة غير منتظمة، وطرقهم معقدة غير واضحة، فنظمها الخوارزمي تنظيما تبناه علم الجبر الحديث، وعالجها بأسلوب واضح، وقد جعل المعلومات المبعثرة مرتبطة ببعضها، تتسلسل تسلسلاً منطقيا من المقدمات الى النتائج، مما جعل علم الجبر الذي اخذه عنه رياضيو اوروبا يرتبط باسمه.

وفي كتاب الجبر والهندسة حلول هندسية من الدرجة الثانية، ونضرب مثلا على احداها، كما ورد في الكتاب.

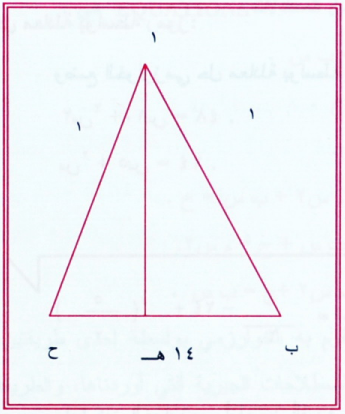
فرض الخوارزمي مثلثا طول اضلاعه : 15، 14، 13، وتوخى حساب مساحته كما يلي :

لتكن

ح هـ = س

ب هـ = 14 – س

²15 – (14 – س)² = ²13 – س²

وينتج أن س = 5

الان 1 هـ 2 = 213 – 25 = 144.

ا هـ 12

المساحة =12x14/2= 84

من جهة اخرى يبين الخوارزمي كيفية ضرب الجذور ببعضها، اما منفردة واما مضافا اليها عدد، واما مطروحا منها عدد واما مطروحة من عدد، كما يبين لنا كيفية جمعها الى بعضها، وكيفية طرحها من بعضها، وذلك بالطرق التي يستخدمها الجبر الحديث.

وعالج الخوارزمي في كتابة مسائل مختلفة تؤدي الى معادلات من الدرجة الثانية، باساليب قريبة من التي نستعملها اليوم، غير انه كان يقتصر على استخراج الجذور الايجابية ولا يعرف كيفية استخراج الجذور السلبية.

ويعالج كتاب الجبر والمقابلة المعاملات التي تجري بين الناس كالبيع والشراء، وصرافة الدراهم، والتأجير، كما يبحث في اعمال مسح الارض فيعين وحدة قياس، ويقوم باعمال تطبيقية تتناول مساحة بعض السطوح plans، ومساحة الدائرة circle ومساحة قطعة الدائرة، segment circulaire وقد عين لذلك قيمة النسبة التقريبية

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد

مواضيع ذات صلة

يوحنا القس

يعيش بن ابراهيم الاندلسي

يحيى بن إسماعيل

ولف – جون كريستان بارون فون

ورنسكي – جوزيف ماري هوهن

واينتشر – الفريد نورث

وايل اندريه

وايتناوي – هاسلر

واليس – جون

رون – السير كريستوفر

الواسطي

هيلبرونر – بول