

علم الكيمياء

تاريخ الكيمياء والعلماء المشاهير

التحاضير والتجارب الكيميائية

المخاطر والوقاية في الكيمياء

اخرى

مقالات متنوعة في علم الكيمياء

كيمياء عامة


الكيمياء التحليلية

مواضيع عامة في الكيمياء التحليلية

التحليل النوعي والكمي

التحليل الآلي (الطيفي)

طرق الفصل والتنقية


الكيمياء الحياتية

مواضيع عامة في الكيمياء الحياتية

الكاربوهيدرات

الاحماض الامينية والبروتينات

الانزيمات

الدهون

الاحماض النووية

الفيتامينات والمرافقات الانزيمية

الهرمونات


الكيمياء العضوية

مواضيع عامة في الكيمياء العضوية

الهايدروكاربونات

المركبات الوسطية وميكانيكيات التفاعلات العضوية

التشخيص العضوي

تجارب وتفاعلات في الكيمياء العضوية


الكيمياء الفيزيائية

مواضيع عامة في الكيمياء الفيزيائية

الكيمياء الحرارية

حركية التفاعلات الكيميائية

الكيمياء الكهربائية


الكيمياء اللاعضوية

مواضيع عامة في الكيمياء اللاعضوية

الجدول الدوري وخواص العناصر

نظريات التآصر الكيميائي

كيمياء العناصر الانتقالية ومركباتها المعقدة


مواضيع اخرى في الكيمياء

كيمياء النانو

الكيمياء السريرية

الكيمياء الطبية والدوائية

كيمياء الاغذية والنواتج الطبيعية

الكيمياء الجنائية


الكيمياء الصناعية

البترو كيمياويات

الكيمياء الخضراء

كيمياء البيئة

كيمياء البوليمرات

مواضيع عامة في الكيمياء الصناعية

الكيمياء الاشعاعية والنووية
Crystal field theory
المؤلف:
CATHERINE E. HOUSECROFT AND ALAN G. SHARPE
المصدر:
INORGANIC CHEMISTRY
الجزء والصفحة:
2th p 557
19-8-2016
6047
Crystal field theory
A second approach to the bonding in complexes of the d-block metals is crystal field theory. This is an electrostatic model and simply uses the ligand electrons to create an electric field around the metal center. Ligands are considered as point charges and there are no metal–ligand covalent interactions.
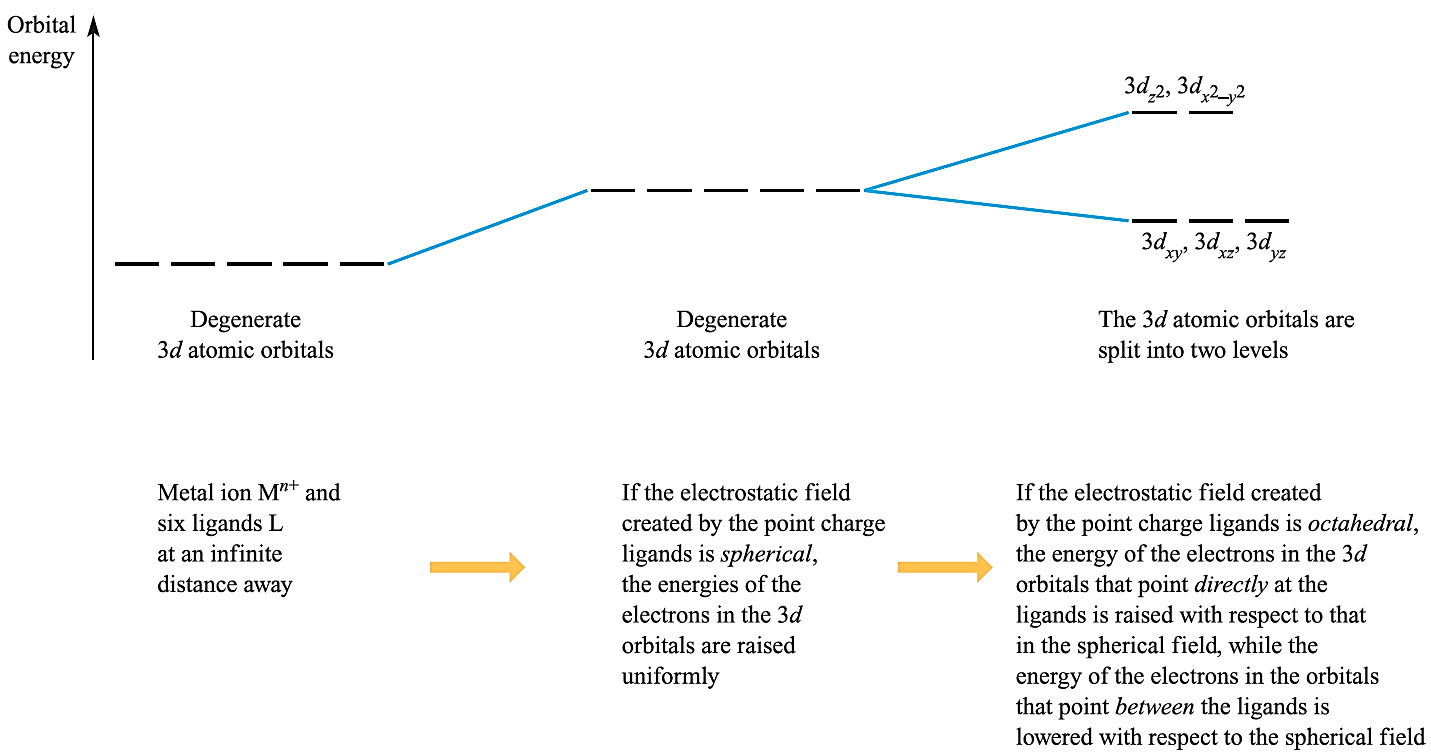
Fig. 1.1 The changes in the energies of the electrons occupying the d orbitals of an Mn+ ion when the latter is in an octahedral crystal field. The energy changes are shown in terms of the orbital energies.
The octahedral crystal field
Consider a first row metal cation surrounded by six ligands placed on the Cartesian axes at the vertices of an octahedron (Figure 1.1a). Each ligand is treated as a negative point charge and there is an electrostatic attraction between the metal ion and ligands. However, there is also a repulsive interaction between electrons in the d orbitals and the ligand point charges. If the electrostatic field (the crystal field) were spherical, then the energies of the five 3d orbitals would be raised (destabilized) by the same amount. However, since the dz2 and dx2-y2 atomic orbitals point directly at the ligands while the dxy, dyz and dxz atomic orbitals point between them, the dz2 and dx2-y2 atomic orbitals are destabilized to a greater extent than the dxy, dyz and dxz atomic orbitals (Figure 1.1). Thus, with respect to their energy in a spherical field (the barycentre, a kind of ‘centre of gravity’), the dz2 and dx2-y2 atomic orbitals are destabilized while the dxy, dyz and dxz atomic orbitals are stabilized.
Crystal field theory is an electrostatic model which predicts that the d orbitals in a metal complex are not degenerate. The pattern of splitting of the d orbitals depends on the crystal field, this being determined by the arrangement and type of ligands. It can be deduced that the dz2 and dx2-y2 orbitals have eg symmetry, while the dxy, dyz and dxz orbitals possess t2g symmetry (Figure 1.2). The energy separation between them is Δoct (‘delta oct’) or 10Dq. The overall stabi-lization of the t2g orbitals equals the overall destabilization of the eg set. Thus, orbitals in the eg set are raised by 0.6 Δoct with respect to the barycentre while those in the t2g set are lowered by 0:4Δoct. Figure 1.2 also shows these energy differences in terms of 10Dq.
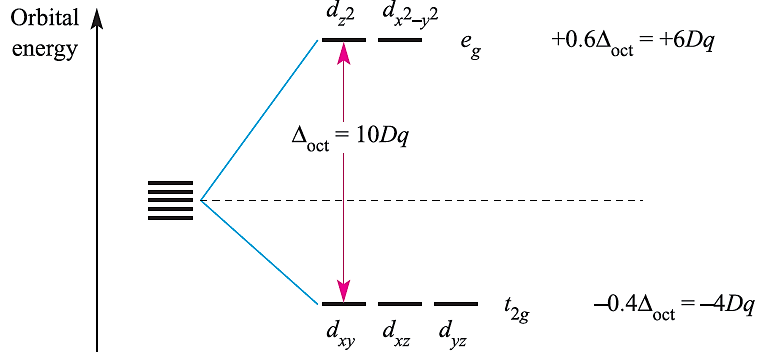
Fig. 1.2 Splitting of the d orbitals in an octahedral crystal field, with the energy changes measured with respect to the barycentre.
Both Δoct and 10Dq notations are in common use, but we use Δoct in this book. The stabilization and destabilization of the t2g and eg sets, respectively, are given in terms of Δoct . The magnitude of Δoct is determined by the strength of the crystal field, the two extremes being called weak field and strong field (equation 1.1).
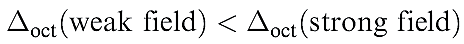 (1.1)
(1.1)
It is a merit of crystal field theory that, in principle at least, values of Δoct can be evaluated from electronic spectroscopic data . Consider the d1 complex [Ti)H2O(6]3+, for which the ground state is represented by diagram 1.2 or the notation t2g 1eg0.
 (1.2)
(1.2)
The absorption spectrum of the ion (Figure 1.3) exhibits one broad band for which λmax = 20300 cm-1 corresponding to an energy change of 243 kJ mol-1. (The conversion is 1 cm-1 = 11.96 ×10-3 kJ mol-1.) The absorption results from a change in electronic configuration from t2g 1eg0 to t2g0 eg1, and the value of λmax (see Figure 20.15) gives a measure of Δoct. For systems with more than one d electron, the evaluation of Δoct is more complicated; it is important to remember that Δoct is an experimental quantity. Factors governing the magnitude of Δoct (Table 1.2) are the identity and oxidation state of the metal ion and the nature of the ligands.
We shall see later that Δ parameters are also defined for other ligand arrangements (e.g. Δtet). For octahedral complexes, Δoct increases along the following spectrochemical series of ligands; the [NCS]- ion may coordinate through the N- or S-donor (distinguished in red below) and accordingly, it has two positions in the series:
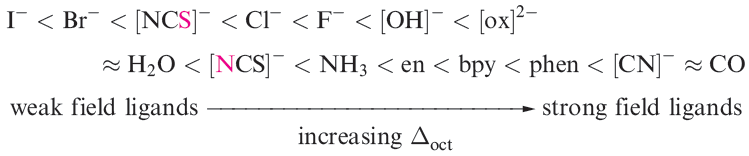
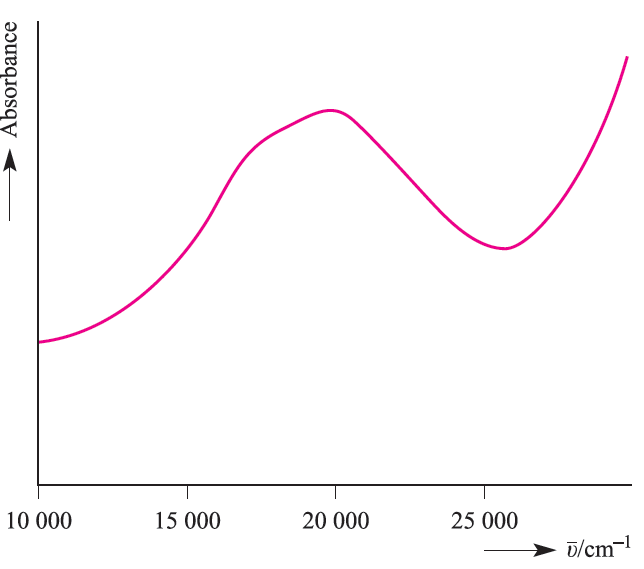
Fig. 1.3 The electronic spectrum of [Ti(H2O)6]3+ in aqueous solution.
The spectrochemical series is reasonably general. Ligands with the same donor atoms are close together in the series. If we consider octahedral complexes of d-block metal ions, a number of points arise which can be illustrated by the following examples:
- the complexes of Cr(III) listed in Table 1.2 illustrate the effects of different ligand field strengths for a given Mn+ ion;
- the complexes of Fe(II) and Fe(III) in Table 1.2 illustrate that for a given ligand and a given metal, Δoct increases with increasing oxidation state;
Table 1.2 Values of Δoct for some d-block metal complexes.
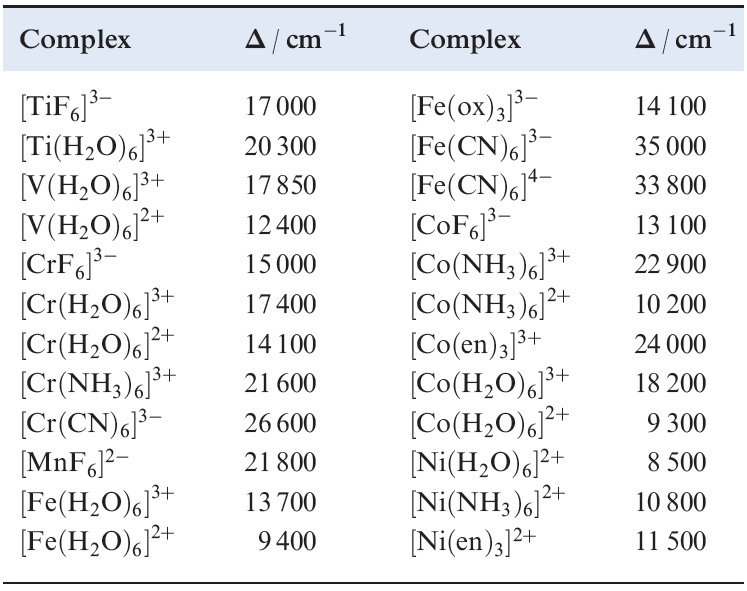
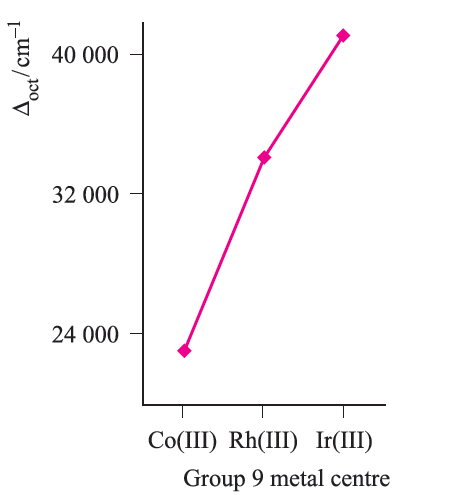
Fig. 1.4 The trend in values of Δoct for the complexes [M(NH3)6]3+ where M = Co, Rh, Ir.
- where analogous complexes exist for a series of Mn+ metals ions (constant n) in a triad, Δoct increases significantly down the triad (e.g. Figure 1.4);
- for a given ligand and a given oxidation state, Δoct varies irregularly across the first row of the d-block, e.g. over the range 8000 to 14 000 cm-1 for the [M)H2O)6]2+ ions.
Trends in values of Δoct lead to the conclusion that metal ions can be placed in a spectrochemical series which is independent of the ligands:
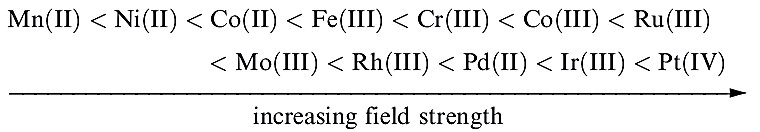
Spectrochemical series are empirical generalizations and simple crystal field theory cannot account for the magnitudes of Δoct values.
 الاكثر قراءة في نظريات التآصر الكيميائي
الاكثر قراءة في نظريات التآصر الكيميائي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















