The main theorem that we present in this section is very important, for it is closely related to several results from other areas of graph theory. We will discuss a few of these areas after we have proven the theorem. A set C of vertices in a graph G is said to cover the edges of G if every edge of G is incident with at least one vertex of C.

Such a set C is called an edge cover of G.

Consider the graphs G₁ and G₂ in Figure 1.1. In G₁,theset {b, d, e, a} is an edge cover, as is the set {a, e, f}. In fact, you can see by a little examination that there is no edge cover G₁ with fewer than three vertices. So we can say that {a, e, f} is a minimum edge cover of G₁.In G₂, each of the following sets is an edge cover: {v₁,v₂,v₃,v₄,v₅,v₆} (obviously) and {u₂,v₆,u₁}. What is the size of a minimum edge cover here?

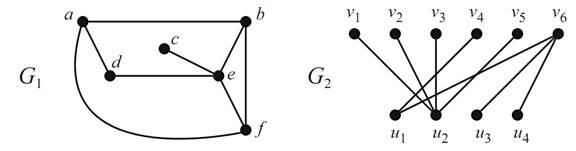
                                             FIGURE 1.1.

We are now ready to prove the following result of K¨ onig [2] and Egerva´ ry[3].

Theorem1.1 (König–Egerva´ ry Theorem).

Let G be a bipartite graph. The maximum number of edges in a matching in G equals the minimum number of vertices in an edge cover of G.

Proof. Let M be a maximum matching of G. Let X and Y be the partite sets of G,and let W be the set of all M-unsaturated vertices of X (see Figure 1.2).

Note that |M| = |X|−|W|.

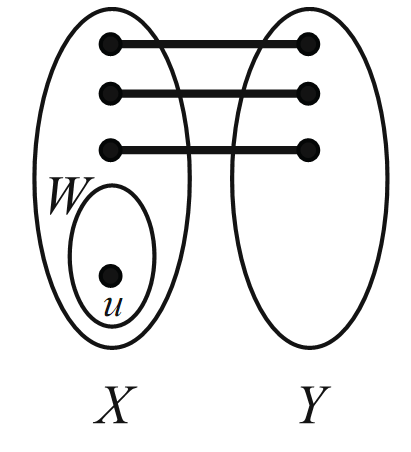
                        FIGURE 1.2.

Now let A be the set of vertices of G that can be reached via an M-alternating path from some vertex of W. Let S = A ∩ X, and let T = A ∩ Y . We can note two things now: First, S W is matched to T (implying that |W| = |S|−|T |), and second, N(S)= T .

If we let C =(X S) ∪ T , we see that C covers the edges of G. So C is an edge cover of G, and |C| = |X|−|S| + |T | = |X|−|W| = |M|. Now suppose that C^/ is any edge cover. Since each vertex of C--------- can cover at most one edge of M, it must be that |C^/ |≥|M|. We conclude then that C is a minimum edge cover.

The König–Egerva´ ry Theorem is one of several theorems in graph theory that relate the minimum of one thing to the maximum of something else. What follows are some examples of theorems that are very closely related to the König–Egerva´ ry Theorem.

Menger’s Theorem

Let G be a connected graph, and let u and v be vertices of G.If S is a subset of vertices that does not include u or v, and if the graph G − S has u and v indifferent connected components, then we say that S is a u, v-separating set. The following result is known as Menger’s Theorem [4].

Theorem 1.2.

 Let G be a graph and let u and v be vertices of G. The maximumnumber of internally disjoint paths from u to v equals the minimum number of vertices in a u, v-separating set.

Max Flow Min Cut Theorem

A graph can be thought of as a flow network, where one vertex is specified to be the source of the flow and another is specified to be the receiver of the flow. As an amount of material flows from source to receiver, it passes through other intermediate vertices, each of which has a particular flow capacity. The total flow of a network is the amount of material that is able to make it from source to receiver.A cut in a network is a set of intermediate vertices whose removal completely cuts the flow from the source to the receiver. The capacity of the cut is simply the sum of the capacities of the vertices in the cut.

Theorem 1.3.

Let N be a flow network. The maximum value of total flow equals the minimum capacity of a cut.

Independent Zeros

If A is an m × n matrix with real entries, a set of independent zeros in A can be thought of as a set of ordered pairs {(i₁,j₁), (i₂,j₂),..., (i_t,j_t)} with the following properties:

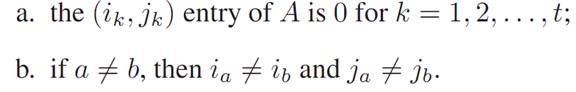
That is, none of the zeros in the set are in the same row or column. Now, in this matrix A one can draw lines through each row and column that contains a zero. Such a set of lines is said to cover the zeros of A.

Theorem 1.4.

 The maximum number of independent zeros in A is equal to the minimum number of lines through rows or columns that together cover all the zeros of A.

_______________________________________________________________________________

1-Combinatorics and Graph Theory, Second Edition, John M. Harris • Jeffry L. Hirst • Michael J. Mossinghoff,2000,page(108-11)

2-D. König, Graphen und Matrizen, Math. Fiz. Lapok 38 (1931), 116–119.

3- E. Egerva´ ry, Matrixok Kombinato´ rius Tulajdonsa´ gairo´ l,Mat.Fiz.Lapok 38 (1931), 16–28..

4-K. Menger, Zur allgemenen Kurventheorie, Fund. Math. 10 (1927), 95–115.

اخر الاخبار

اخبار العتبة العباسية المقدسة

المجمع العلمي يقيم برنامجًا قرآنيًّا رمضانيًّا في جامعة الكوفة

الحلقة 21 من جائزة العميد القرآنية تشهد تأهل القارئ محمد حسن زاده من أفغانستان إلى المرحلة النهائية

موكب أهالي كربلاء يحيي ذكرى شهادة الإمام علي (عليه السلام) عند مرقده الطاهر

لليوم الثالث.. شعبة الخطابة تنظم مجالس العزاء لإحياء ذكرى شهادة الإمام علي (عليه السلام)

المزيد

الآخبار الصحية

تأثير اللياقة البدنية على الدماغ

تجربة سريرية تظهر فوائد اللوز للمصابين بالسمنة

اكتشاف طريقة غير متوقعة لتقليل خطر الإصابة بالسكري

خمسة مؤشرات صحية مهملة قد تنقذ حياتك

المزيد

الآخبار التكنلوجية

علماء الجيولوجيا يفكون لغز الصدع العملاق تحت الماء في المحيط الأطلسي

تحذير جديد: الاحترار العالمي يتسارع وقد نكسر حاجز 1.5 درجة قبل 2030

الصين تكشف عن ألياف كربون تفوق قوة الفولاذ بـ10 مرات

الجهاز المناعي يظهر دورا غير متوقع في صحة العظام

المزيد

مواضيع ذات صلة

Minimum Spanning Tree

Maximum Leaf Number

Lobster Graph

Labeled Tree

Internal Path Length

Red-Black Tree

Pseudotree

Pseudoforest

Prüfer Code

Planted Tree

Planted Planar Tree

Graph Strength