
Connectivity-k-edge-connected graphs
 المؤلف:
Jean-Claude Fournier
المؤلف:
Jean-Claude Fournier
 المصدر:
Graph Theory and Applications
المصدر:
Graph Theory and Applications
 الجزء والصفحة:
65
الجزء والصفحة:
65
 28-7-2016
28-7-2016
 2133
2133
The following concept corresponds to the k-connected concept defined above. A graph G is k-edge-connected if 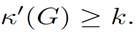
We have an “edge” version of Menger’s theorem, which we equally accept:
Theorem 1.1 (Menger, edge statement).
A simple graph G is k-edge-connected if and only if any two distinct vertices are connected by k edge-disjoint paths (that is pairwise without common edges).
Note. The first inequality of proposition(For any simple graph G, we have: 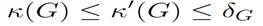 )
)
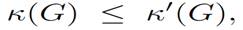 is easily deduced from both statements of Menger’s theorem. Put
is easily deduced from both statements of Menger’s theorem. Put 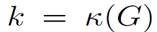
consider any two given vertices of G, x and y. There are k vertex-disjoint paths linking x and y according to Menger’s vertex statement. Therefore there is at least the same number of edge-disjoint paths linking x and y, since
the vertex-disjoint property for paths implies the edge-disjoint property. This leads to Gk-edge-connected and the inequality 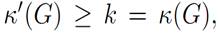 from Menger’s edge statement. This inequality
from Menger’s edge statement. This inequality 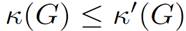 is in fact natural if we observe that the removal of a vertex in a graph causes the removal of all incident edges and thus generally has a greater impact on the connectivity of the graph than the removal of a single edge.
is in fact natural if we observe that the removal of a vertex in a graph causes the removal of all incident edges and thus generally has a greater impact on the connectivity of the graph than the removal of a single edge.
Graph Theory and Applications ,Jean-Claude Fournier, WILEY, page(65)
 الاكثر قراءة في نظرية البيان
الاكثر قراءة في نظرية البيان
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


