

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Coloring-Algorithmic aspects
المؤلف:
Jean-Claude Fournier
المصدر:
Graph Theory and Applications
الجزء والصفحة:
73-75
27-7-2016
2340
The problem of the chromatic index of a simple graph is a remarkable example of an NP-complete problem (even when the NP-completeness has been found much later than for other graph problems). Indeed, deciding if the chromatic index of a simple graph is Δ or Δ + 1 is an NP-complete problem.
Nevertheless, the problem of finding in a simple graph a maximum matching, that is one having the largest number of edges possible, can be solved by a polynomial algorithm. Indeed, it is with this problem that the concept of polynomial complexity was introduced. It is then possible to think of the following algorithm to find the chromatic index of a graph, this index being seen here as the lowest number of classes of a partition of edges into matchings: consider a maximum matching C1 of G, and then a maximum matching C2 of G − C1, the graph obtained by removing the edges of C1, and so on until the removal of all edges of G. The matchings successively obtained, C1,C2,... of G, construct an edge partition into matchings of the graph. We have tried to minimize the number of these matchings by considering each time a matching with a maximum number of edges in what was left. This way of proceeding means giving a first color as often as possible to some edges of the graph, while respecting the condition of never giving the same color to two edges sharing the same end vertex. We then give a second color to a maximum number of edges not yet colored, and so forth until all edges of the graph are colored. Unfortunately, this greedy algorithm (see Chapter of tree) in general does not yield an optimal result, that is, a coloring with the lowest possible number of colors, as shown in Figure 1.1.
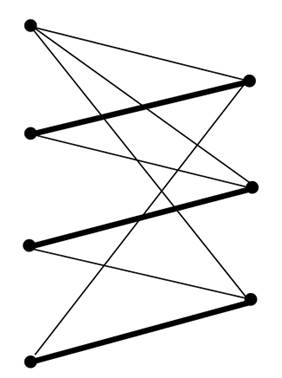
Figure 1.1. By giving a first color to the edges of the maximum matching shown in bold, it will not be possible to have a Δ-coloring of this bipartite graph of maximum degree 3 (because of the degree 3 vertex on the upper left).
Nevertheless such a coloring exists It is always possible to try every way of giving colors to the edges to find a coloring. There is a general classic method called backtracking. It equates to a depth–first search of an arborescence (an algorithm studied in Chapter of Search Algorithms). In fact it is a very good anticipation exercise to try to implement this search for the chromatic index of the graph, called the Petersen graph, shown in Figure 1.2. This graph does not have a Δ-coloring; its chromatic index is not 3 but 4.
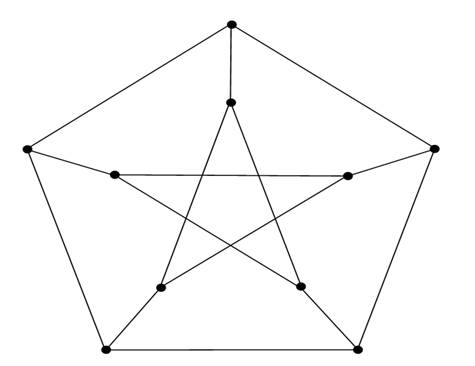
Figure 1.2. Petersen’s graph (chromatic index =4)
In fact, there is no other real general method known at present to verify that there is no Δ-coloring. However, the number of cases increases exponentially with the size of the graph, showing all too well the difficulty of an NP-complete problem.
The case of bipartite graphs is algorithmically more accessible. It is possible to find with a polynomial algorithm a Δ-coloring of any bipartite graph (simple or not). This is particularly interesting in relation to the timetabling problem. The study of such an algorithm is proposed as an exercise at the end of this chapter.
Graph Theory and Applications ,Jean-Claude Fournier, WILEY, page(73-75)
 الاكثر قراءة في نظرية البيان
الاكثر قراءة في نظرية البيان
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















