Many applications are modeled by graphs with edges which are oriented, the endvertices of the edge not playing a symmetric role.

They are called directed graphs. Among them, two classes are particularly important: directed graphs without circuits and arborescences, the latter being commonly called “trees” in, for example, computer science.

1.1 Definitions and basic concepts

A directed graph, abbreviated to digraph, G, is defined by two finite sets: a non-empty set X of vertices and a set A of arcs, or directed edges, with an ordered pair (x, y) of vertices which are the endvertices of a, associated with each arc. Vertex y is called the head and vertex x is called the tail.

1.1.1 Notation

We write G =(X,A). Sets X and A may also be denoted by X(G)and A(G). We keep, as in the undirected case, the notations n_G or n for the number of vertices and m_G or m for the number of arcs.

1.1.2 Terminology

When (x, y) is the ordered pair of endvertices associated with arc a,we say that arc a joins vertex x to vertex y, that arc a is incident to vertices x and y, or more specifically that arc a comes out of vertex x and that it enters into vertex y .Vertex y is called a successor of x and vertex x is called a predecessor of y. As with graphs, we have a loop in the case of equality x = y, and a multiple arc in the cases of arcs having an identical ordered pair  (x, y) associated with them. It is possible to specify, according to the number of arcs involved: double arc, triple arc, etc. Two arcs of which the associated ordered pairs are respectively (x, y)and(y,x) are said to be opposed.

A digraph is said to be strict if it has no loops and no multiple arcs (it may have opposed arcs). In this case, often encountered, each arc is identified by the ordered pair of its endvertices, which are then distinct, and we write, for example, a =(x, y). For a strict digraph G =(X,A), we can define the set of the arcs A directly as a subset of the Cartesian product X × X.

           A strict digraph is symmetric if for any arc (x, y) there is also the opposed arc (y,x). This concept is very close to that of a graph.

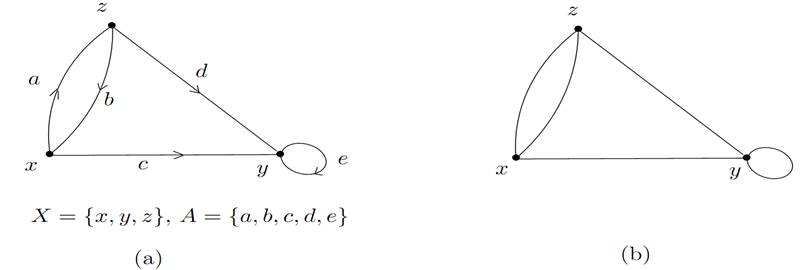
Figure 1. 1 (a) A digraph: the arc a is associated with the ordered pair (x, z), b with the ordered pair (z,x), c with the ordered pair (x, y), d with the ordered pair (z, y),and e with the ordered pair (y, y); (b) the underlying graph

1.1.3 Representation

As we saw in Figure 1.1(a), digraphs are drawn in a plane as graphs, with simply an arrow indicating its orientation on each arc line, the arrow going from x to y if the ordered pair (x, y) is associated with it. Finally, to complete the definition of digraphs, it should be noted that the digraphs under consideration are unlabeled digraphs, that is, considered up to isomorphism. We will not go back over this concept which can be defined with graphs and does not pose any practical problem.

1.1.4 Underlying graph

Given a digraph G we consider the underlying graph, obviously defined by “forgetting” the orientation of the arcs of G, that is that each arc with which the ordered pair (x, y) is associated is replaced by an edge of which the associated pair of endvertices is xy (see Figure 1.1(b)).

Note. Given a graph G there are 2^m digraphs for which the underlying graph is G (m being the number of edges of G).

All concepts defined for graphs also apply to digraphs by means of the underlying graph: degree of a vertex, connectedness and connected components, walk, trail, path, etc. For example, we say that a digraph is connected if its underlying graph is connected. These concepts are therefore independent from the orientation of the arcs. There are also other concepts which take into account the orientation of the arcs and which we are now going to define.

1.1.5 “Directed” concepts

Some concepts can be transposed directly from the undirected to the directed case by replacing the word edge by the word arc. These are: sub digraphs, induced sub digraphs, spanning sub digraphs, directed walks, directed trails, directed paths and directed cycles, which we also call circuits.

For example, a directed walk is a sequence of elements, alternately vertices and arcs beginning and ending with a vertex, and such that each arc has for its tail the preceding vertex in the sequence and for its head the following vertex. The first and the last vertices are the ends. A directed cycle, or circuit, is a closed directed path of length ≥ 1 (its ends coincide). We say that a directed walk or a directed cycle goes through an arc or a vertex if it contains this arc or vertex. The length of a directed walk or a directed cycle is the number of its arcs. As with graphs, a directed walk in a digraph may have zero length but a cycle must have a length ≥ 1.

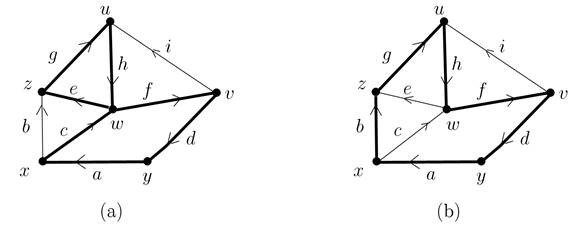
Figure1.2. A strict directed graph, with, in bold: (a) a directed closed trail (x, c,w, e, z, g,u,h,w, f, v, d, y, a,x); (b) a circuit (x, b, z, g, u, h,w, f, v, d, y, a, x)

The following concepts have a definition specific to the directed case.

1.1.6 In degrees and out degrees

The indegree of a vertex x of a digraph G is the number of arcs entering into x .The outdegree of x is the number of arcs exiting from x. These are denoted by d⁻_G(x), or d⁻(x), and d⁺_G(x), or d⁺(x), and are integers. It is easily seen that:

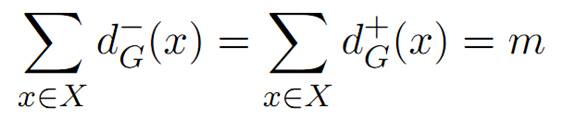
Loops are not often considered in digraphs, nevertheless this formula correctly accounts for them, knowing that each loop in a digraph counts for one unit of outdegree and one unit of indegree of the vertex under consideration. We again find the formula for the sum of the degrees given in of Basic Concepts, in observing that for each vertex x we have: d_G(x)= d⁻ _G(x)+d⁺_G(x), so:

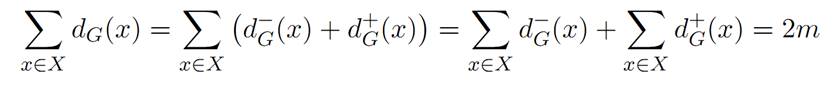
A digraph G is strongly connected if for any two distinct vertices x and y there is a directed path going from x to y. Note that as this definition is symmetric in x and y, there is also a directed path from y to x.

A strongly connected component of G is a maximal strongly connected induced subdigraph of G. Maximal means that there is no strongly connected induced subdigraph containing strictly (for the vertices) this subdigraph. These components may also be defined as being the subdigraphs induced by the classes of the following equivalence relation on the vertices: there is a directed path from x to y and a directed path from y to x. These components define a partition of the set of the vertices (but not of the arcs) and constitute decomposition into strongly connected components of G. This decomposition is unique.

The strongly connected components are less simple to determine than the connected components, but there are nevertheless good algorithms (of linear complexity) for finding them.

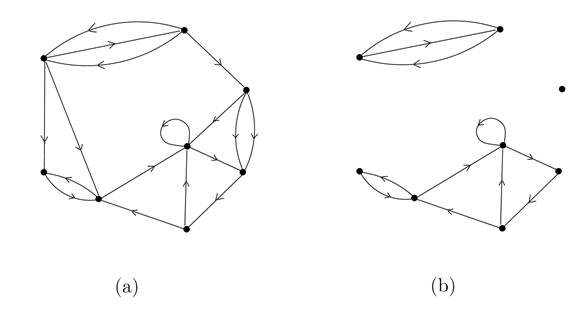
Figure 1.3. (a) A digraph which is not strongly connected; (b) its three strongly connected components (note that one of them is reduced to a vertex)

Note. Vertices belonging to the same circuit belong to the same strongly connected component (justify).

1.1.8 Representations of digraphs inside a machine

The same principle used to represent a (undirected) graph inside a machine can be applied to digraphs, with a few additional specifications because of orientation.

1. The adjacency matrix M =(m_ij ) of a digraph G =(X,A), with X = {x₁,...,x_n}, is defined by putting m_ij equal to the number of arcs of which the associated ordered pair is (x_i,x_j ). Contrary to the undirected case, this square matrix is not usually symmetric (but it is the case with a symmetric digraph).

2. The data for the neighborhood of each vertex can be given by lists of successors: each list associated with a vertex contains the successors of that vertex. Classically, it is possible to implement these lists as linked lists. In concrete terms, a table indexed on the vertex type contains for each vertex an access pointer to its list of successors. For some applications  the digraph is more naturally represented by lists of predecessors. Each vertex is associated with the list of its predecessors. It is not very hard to go from one to the other, that is from successors’ lists to predecessors’ lists and vice versa (write the corresponding algorithms).

Another way to model a digraph using the neighborhoods of its vertices (which we will use in Chapter 8 for flows) is to give for each vertex the set of arcs exiting from this vertex and the set of arcs entering this vertex.

3. The list of arcs constitutes the third principle of the implementation of digraphs. In concrete terms, it is also possible to have an array indexed on the type arc, the arcs being numbered from 1 to m, with the ordered pair of its endvertices associated with each arc. These data can be given in a record composed of two fields, in the order: the tail of the arc, then its head.

The advantages and inconveniences of these various representations, in particular the memory space required, can be analyzed as in the case of graphs.

Figure 1.4 illustrates these representation principles.

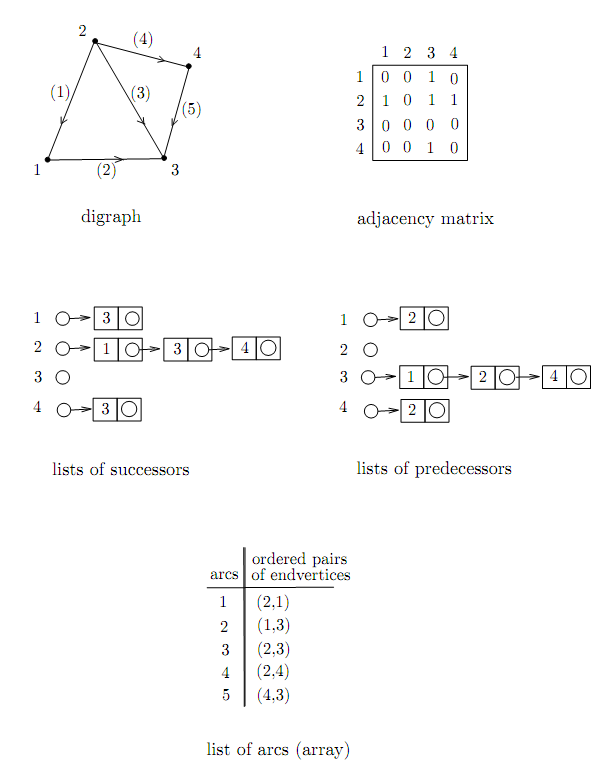
Figure 1.4. Different representations of a (strict) digraph

We also consider weighted digraphs: G =(X,A) with a mapping v : A →R. The implementing of these digraphs by an adjacency matrix, when they are strict, is generally well suited: each entry of the matrix is the value of the corresponding arc. The implementing by list of arcs can also be adapted but in practice the choice is made depending on the entry in the digraph required by the algorithm.

Graph Theory  and Applications ,Jean-Claude Fournier, WILEY, page(83-90)