The so-called Chinese postman problem (thus called because of the nationality of the first person to be interested by it) is typically an optimal tour problem. It means, for example, touring all streets of a town while minimizing the total distance covered.
In graph terms, the general problem is as follows: given a graph G with edges weighted with values ≥ 0, we have to find a closed walk of G going at least once through each edge of G, and for which the sum of the values of its edges is as small a possible. Let us specify that in general this closed walk is not a closed trail, which means that an edge of the graph may appear in it several times. Thus, the minimum total value can be greater than the sum of the values of all the edges of the graph because of the edges covered several times. In the particular case of a Euler tour, we have equality, since a Euler tour is then a solution to the problem. When the graph is not Eulerian, while still supposed connected, a closed walk solution must necessarily go more than once through at least one edge of the graph. It is all a matter of choosing these multiple edges in such a way as to minimize the sum of their values. Let us make this more specific. In what follows we will write CPP for “Chinese Postman Problem”.
Let G =(X,E) be a connected graph weighted by v : E → R+. Let us put Y the set of the odd (degree) vertices of G, supposed non-empty. We first have:
– A closed walk of G corresponds to a set F of edges defined on X, which is disjoint from E and which verifies the two following properties:
1) any edge of F is parallel to an edge of E,
2) graph H =(X,F) has the same set, Y , of odd vertices as G.
Given a closed walk D of G, consider the set F composed in the following manner: for any edge e of G appearing m(e) > 1 times in D, put in F m(e) − 1 edges parallel to e. It is easy to verify that this set F verifies the two preceding properties. In particular the second one is linked to the fact that graph G + F =(X,E ∪ F) is Eulerian: it is indeed possible to define a Euler tour of G + F by searching walk D and by doubling each edge of G met a second time, which comes back to construct G + F. The vertices of G + F are therefore of even degree, which implies that graphs G and H have the same odd-degree vertices (an odd vertex in one set is also odd in the other because the sum of these degrees is even). Conversely, given a set F verifying the preceding properties, graph G + F is Eulerian because it is connected and its vertices are even-degree vertices, and a Euler tour of this graph defines, in an obvious manner, a closed walk of G (by repeating in G the edges doubled in G + F).
Let us now suppose that the edges of set F are weighted, each with the same value as the edge of G to which it is parallel. We add the third following property:
3) the value 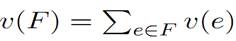 is minimal.
is minimal.
This property is equivalent to the next one, which defines an optimal solution of the CPP in G, where D is the closed walk associated with set F as previously:
3’) the value  is minimal.
is minimal.
Let us specify that the sum which defines v(D) is taken on the sequence of the edges of walk D, that is, an edge is counted as many times as it
appears in this walk. This equivalence between properties 3 and 3’ comes directly from the equality v(D)= v(E)+ v(F) and from the fact that the
value  is constant.
is constant.
We can reformulate what has been described above by saying that a solution D of the CPP in G corresponds to a set F of edges which verifies the preceding properties 1, 2 and 3. We are going to characterize set F in a manner which will show how to obtain it. Let us make d the distance function in (weighted) graph G, that is, d(x, y) is the distance between the vertices x and y. Let KY be the complete graph defined on the vertices set Y (odd vertices of G), weighted on the edges by d, which means that edge xy of KY has the value d(x, y). We have:
– Set F verifies the preceding properties 1, 2, and 3 if and only if it corresponds to a minimum matching of KY .
Let us further explain this correspondence between F and a matching of KY . Let us suppose that F verifies properties 1, 2, and 3. Let us consider in H =(X,F) a vertex x1 of odd degree. According to an easy result, there is another vertex of odd degree in H; letitbe x/1, linked to x1 by a walk μ1,whichwecan suppose to be a path. Let us put H1 = H − F(μ1), where F(μ1) designates the set of the edges of μ1.In H1, vertices x1 and x/1 are even-degree vertices.
If H1 still has an odd-degree vertex, then we start again with this graph, by defining a path μ2 which links two odd-degree vertices x2 and x/2.We continue until at last graph Hk is reduced to two odd vertices xk and x/k linked by a path μk. We thus have k paths of H (Hi are spanning subgraphs of H) which are pairwise disjoint for the edges, and which “match” the odd-degree vertices of H; these are also those of G since they are the same vertices according to property 2 (remember that a graph always has an even number of odd vertices). It easily follows from the minimality of v(F)that each path μi must be a shortest path between the vertices xi and x/I which it is linking (otherwise it would suffice to replace this path by a shorter one).
It is therefore possible to associate with each path μi the edge xix/iof KY , with its value d(xi,x/I ). This thus defines a matching M of KY associated with the set of the preceding paths. We have l(μi), the length of path μi:

Conversely, given a matching M of KY , it is easy to associate with it a m set F verifying the above properties 1 and 2 by considering some parallel edges for all the edges of the paths which correspond in G to the edges of M. With this set F associated with a matching M of KY ,we have the equality v(F)= v(M). Thus the value of v(F) is minimal, that is it verifies property 3, if and only if set F is associated with a minimum matching M.
We thus see how to obtain a set F of edges corresponding to a solution of the CPP in G from a minimum matching of KY . All this leads us to the following algorithm.
1.1 The Edmonds-Johnson algorithm
Let us describe this algorithm step by step.
Step 1: Find for each pair of vertices of odd degree of G a shortest path (in the sense of the weighting of G) which links these vertices.
Step 2: Build a complete weighted graph K of which the vertices are the odd vertices of G, and of which each edge is weighted by the length of the shortest path linking its ends found in step 1. Determine a minimum matching M of K.
Step 3: Build a weighted graph Gˆ by adding in G for each edge of M the edges of the shortest corresponding path (found in step 1). Each added edge is added independently of those already existing. The parallel edges thus created are given the same value by v as those of G.
Step 4: Find a Euler tour of Gˆ. Graph Gˆ corresponds to graph G + F seen above. The Euler tour of Gˆ defines, as we have already seen, a solution of the CPP in G. Let us comment on these different steps. Step 1 can be accomplished by repeatedly using Dijkstra’s algorithm. To find a matching of minimal value in K during step 2, there is a general algorithm not dealt with in this book and more general than the one given in Chapter of(Matchings) which is limited to bipartite graphs. Step 3 is direct. Finally, step 4 is solved by the algorithm previously given in this chapter.
1.2 Complexity
From a complexity point of view, it is possible to verify that this algorithm is, as a whole, polynomial since that is the case for each of its steps. Thus, the Chinese postman problem is solved by a “good” algorithm.
1.3 Example
The number of examples we can give is limited here by the fact that we have not given any general algorithm for finding a matching of minimal value in K during step 2. Nevertheless it is possible to deal with the case where there are few vertices of odd degree. In this case, it is possible to find such a matching directly by considering all possible matchings, which are not numerous (for example, 1 for 2 vertices, 3 for 4 vertices).
In the example given in Figure 1.1, there are only two vertices of odd degree. Its treatment is therefore trivial . At the top of Figure 1.1, see graph G with, in bold, a shortest path joining the two vertices of odd degree x0 andx2. This path was obtained using Dijkstra’s algorithm applied from vertex x0.
At the bottom, observe graph Gˆ obtained by doubling in G the edges of the previous path. All the vertices of this graph are even, therefore it is Eulerian.
It remains to find a Euler tour of Gˆ with one of the algorithms given above. This tour defines a solution to the Chinese postman problem in G (a solution tour goes twice through each of the edges of G in bold).

Figure 1.1. An example of a solution to the Chinese postman problem
Graph Theory and Applications ,Jean-Claude Fournier, WILEY, page(207-211)
 الاكثر قراءة في نظرية البيان
الاكثر قراءة في نظرية البيان
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


