Freeze drying

Freeze drying is a method  for the  removal  of water from  a sample kept at low temperature,  the  water being removed directly from  ice into the vapour phase by sublimation.  It is a non-specific method as all  of the non-volatile solutes are concentrated.

A major use of freeze-drying is for long term storage (preservation) of proteins or other biological samples.  By  reducing the  water content  to  a very low level, microbial growth is inhibited and spoilage of the  stored material is prevented.  Aqueous-phase chemical reactions  are  also inhibited and this  helps to  preserve  the  sample.  It may  be  noted  that  if the water is not removed, a temperature  of ca. -70∞C is  required in order to stop aqueous-phase reactions,  i.e.  a  deep-freeze at  -20C is  not  cold enough.

Freeze drying may destroy the  activity  of some enzymes and, if it is important to retain the activity, this should always be checked before freeze-drying is used to preserve a particular protein.

1.1 Theoretical and practical considerations in freeze-drying

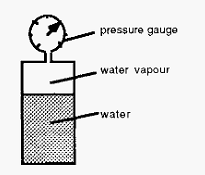
Figure 1. Measurement  of the  vapour pressure  of water.

In order to understand how a freeze-dryer works, it is important  to understand the  concept  of vapour pressure.  What  is “vapour  pressure”? Consider the set-up shown in Fig. 1; a sealed container containing only a liquid (water) and its vapour,  i.e. with no  other gases present,  and with a pressure gauge to monitor the (vapour) pressure.  In  this  way, the  vapour pressure can be measured as the temperature  of the  set-up is changed.  If this is done, it will be noticed that the measured pressure (the vapour pressure) changes with the temperature as shown in Fig. 2.  If there  are other gases present then the  vapour will contribute  a part  of the total pressure, i.e. the total  pressure will be the  vapour  pressure  at  that temperature plus the (partial) pressures of the other gases.

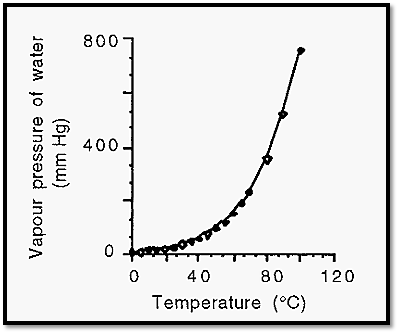
Figure 2. The vapour pressure of water as a function of temperature.

Notice that at 100∞C,  the  standard boiling point of water, the  vapour pressure of water is 760 mm Hg,  which is the  standard  atmospheric pressure. This illustrates the important principle that a liquid will boil when its vapour pressure becomes equal to the  environmental atmospheric pressure.

At ca. 0C (at  pressures of ambient or below), water undergoes a phase change from  a liquid to  a solid, ice.  The vapour pressure of ice is relatively low (compared to that  of water) and is asymptotic to zero as shown in Fig. 3.

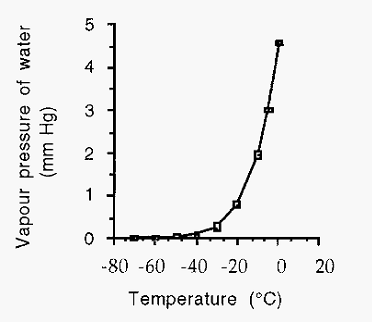
Figure 3. The vapour pressure of ice as a function of temperature.

Just as a liquid will boil when  its  vapour  pressure  becomes  equal  to  the environmental pressure, so a solid will sublime from the  solid state to the vapour state when its vapour pressure becomes equal to the environmental atmospheric pressure.  The salt,  sal ammoniac,  for example, has a vapour pressure higher than 760 mm Hg and thus  sublimes from the  solid to the vapour at  ambient  atmospheric  pressures.  In  order for ice to  sublime, however, it is necessary to  reduce the  pressure to which it is exposed to  values less than  or equal to  its vapour pressure at its particular temperature, e.g. the pressure must be reduced to  1.95  mm Hg, if the ice is at -10C (Fig.  3).

Therefore, consider the  situation illustrated in Fig. 4, where flask A

is at a temperature  T₁ and condenser B is at a temperature  T₂, both T₁and T₂ being below the freezing point of ice but T₁>T₂. It follows then that if P, the overall pressure within the system, is less than VpT₁ (the vapour pressure of ice at  temperature  T₁) and more than VpT₂ (the vapour pressure  of ice  at temperature  T₂), ice will sublime in flask A and condense in B.

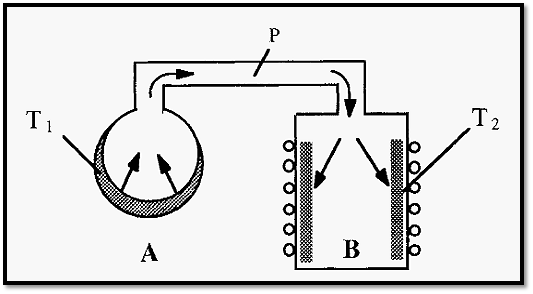
Figure 4. A simple freeze-dryer.

In a practical freeze-dryer, T1  will be about -10∞C and  T2 will be  about -50C. V pT1 will thus be about  1.95 mm Hg and  VpT2 will be about 0.029 mm Hg (Fig. 3). “P”, the pressure measured on the vacuum gauge, must therefore be between  1.95 mm Hg (1,950 microns) and 0.029 mm Hg (29 microns): in practice it is usually between 500 and 100 microns, when the freeze dryer is operating properly.

With regard to the net transport of water vapour from A to B an analogy can be drawn with electricity, i.e. where in electricity,

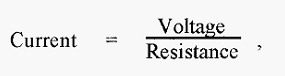
In freeze-drying,

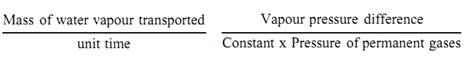
The constant in the “resistance”  term in equation.1  describes  in part the geometry of the piping system connecting flask A and condenser B and is minimal when this is short and wide.  To achieve a maximal rate of freeze-drying, therefore, it is necessary to establish:-

•  A maximal  vapour  pressure  difference  between the  sample and  the condenser,

• a minimum pressure of permanent gases, and,

• a  minimum value of the  piping  geometry constant.

Most of these  factors  are fixed by the  design of a particular machine but it  is useful for the  researcher to  have an  appreciation  of their influence. For example, the first item, considered in conjunction with Fig. 3,  suggests that  there  is no advantage to  be gained in using a condenser temperature  much below -50C,  since  below this  temperature there is little change in the vapour pressure of ice (since it is asymptotic to zero).  A temperature  of  -50C can  be achieved with single-stage refrigeration systems and there is thus little benefit in using expensive two-stage systems to reach a lower condenser temperature.

As ice sublimes from  flask A  it  removes  latent  heat  of sublimation, which keeps the remaining ice cold.  The  heat  removed  by sublimation  is replaced by heat from the  atmosphere,  especially the  latent  heats  of condensation and  freezing of ice condensing on the  outside of the  flask. A thermal gradient  is thus  formed through  the  layers  of ice and the  wall of the  freeze-drying flask (Fig. 5),  and a dynamic equilibrium is established in which the  rate  of heat  input to  the  system  is balanced by the rate of heat loss.  At equilibrium, the  rate  of heat  input  is the  factor limiting the rate of freeze-drying. However, a limit to this rate of input is determined by the point at which the sample melts.

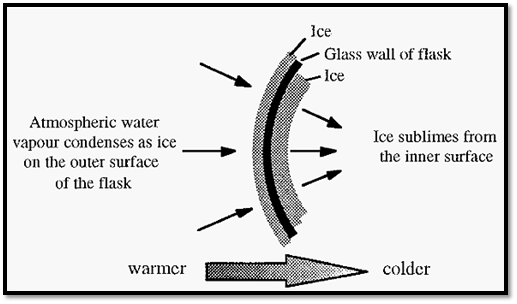
Figure 5. Thermal gradient across a freeze-drying flask and its associated ice layers.

The nature of the system has the following practical ramifications:-

•  The greater the area over which the  sample  is spread, the  greater will be the rate of heat input and the faster will be the rate of freeze-drying;

• The  sample  layer  should be as thin  as possible since  if it  is too  thick there is a risk of the  sample melting on its outermost  surface, due to the thermal gradient.  (Note: If this should happen, the sample should not be re-frozen as the melted sample, being trapped between the  flask wall and the  frozen  part  of the  sample,  might  crack  the  flask  as it expands upon re-freezing.)

•  The  flask  should  be  made  of a material  with  a high  thermal conductivity: thus glass is commonly used. When the freeze-dryer is in operation, there is a flow of heat through the system, as illustrated in Fig. 6.

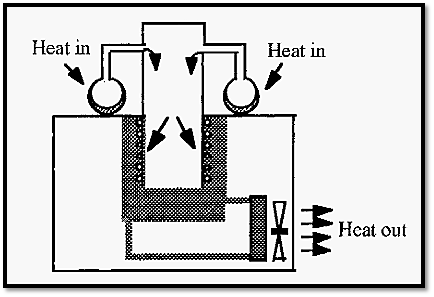
Figure 6. The heat flow through a freeze dryer in operation.

Atmospheric heat enters the  freeze drying flask, via the  ice condensing on the outside of the flask.  The heat is transferred through the flask and is removed by the subliming water vapour.  When this  water vapour condenses,  in the  condenser,  the  heat  is transferred  to  the refrigerant gas and is ultimately returned to the atmosphere  via the radiator of the refrigeration unit.

1.2 Some tips on vacuum

Many people have confused thoughts about vacuums and so a few words on the  subject may  be  useful.  A  vacuum  may  be  defined  as  any pressure less than the  prevailing ambient pressure.  Since vacuums are defined in terms  of a pressure differential,  clear thinking  is easier if one thinks only in terms of pressure, which has a range from  zero to “infinity”.

Ambient pressure is usually about one  atmosphere,  or  760  mm  Hg,  or about 15 p.s.i.  (“p.s.i.”  or pounds per square inch  is  an  old  measure but one which is easy to visualise.  1 p.s.i. ≈ 6.89 kPa).  An absolute vacuum, which is practically unattainable, corresponds to a pressure of zero.  The theoretical maximum pressure differential across the walls of a vessel in the atmosphere but “containing” an absolute vacuum is therefore one atmosphere,  i.e. 760 mm Hg or about  15  p.s.i.  This  is not  a large differential, as pressures go, and there is clearly no truth in the belief that,  “if one  sucks  hard  enough,  almost  any  vessel  can  be  made  to collapse!”

How hard can one suck on water?

Everyone is familiar with the process of drinking water from  a container by using a straw.

Q: Is there a limit to the length of the straw, i.e. to the  height that  the water can be  sucked up?

A: Yes.  In the  case of water the  limit is about 7 metres,  which is the height to which the atmospheric pressure can lift a column of water.  The equivalent height of a column of mercury is 760 mm (do this only as a “thought  experiment”,  though,  since mercury is very toxic!)

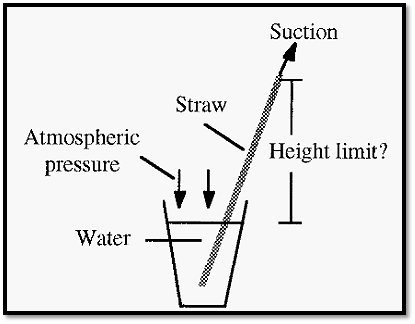
Figure 7. How far can water be sucked up?

This is why farmers have their water pumps near the bottom  of  the valley, near the river. The pump can only “suck” the water up a limited distance (about 7 meters  vertical  height)  but it can push  it up much further than this.

Q: What limits the water from being sucked up higher than 7 meters? A: The water will boil (i.e. be converted to vapour) when the pressure applied to  it  becomes  less than  its  vapour pressure  at  the  prevailing temperature.

In engineering terms  the  point  to  remember  about pressure differentials is that the  resultant force is a function  of the  area over which the  differential  exists.  Consider,  for  example,  the  force  acting upon the Perspex lid of a typical  laboratory  freeze  dryer.  If the  lid is 8 inches  in  diameter  (1  inch  = 2.54  cm)  it  will have  an  area  of ca. 50 square inches.  At a pressure differential of 15 p.s.i., the force acting on the lid is equivalent to ca.  750 pounds weight (ca.  340 kg): no wonder it

bows inward.  If  one  could  get  a  good  enough  grip,  one  could  lift  the entire machine by its lid once the vacuum was established!

On the other hand, what is a high  vacuum and how is it different  to  a “non  -high vacuum”? An atmosphere corresponds to a pressure of 760 mm  Hg.  A  pressure  of  1  mm  Hg  is  not  really  in  the  high  vacuum range but the force applied to  the  system would be  of the  ultimate force. High vacuum pumps “split” the last mm of Hg and 0.5 mm Hg (500 microns) requires a high-vac pump, but the forces on the system will increase by only 0.5/760 or 0.07%, a negligible amount!

A generalization can therefore be made: that if a system  is structurally strong enough to withstand a moderate  vacuum of 1 mm Hg (1000 microns) it will probably withstand any possible high vacuum!  (Remember that attaining high vacuums is like splitting hairs!).  In practical terms this means that one should not  be too  nervous of flasks imploding under vacuum. A flask is more likely to break due to thermal stress or mechanical abuse (point impacts) than under vacuum loads per se.

Nevertheless one should be aware that the likelihood of a flask failing, from whatever cause, increases with the size of the flask.

References

-Dennison, C. (2002). A guide to protein isolation . School of Molecular mid Cellular Biosciences, University of Natal . Kluwer Academic Publishers new york, Boston, Dordrecht, London, Moscow .