Assays for activity of peroteins 

Most proteins  have some  form  of unique functional  activity,  which defines the specific protein and may  be used to  elaborate  an  assay for  its detection and quantitation.  A philosophical  point  to  note  is that  it  is necessary to conceive of an activity and to devise an appropriate  assay, before the protein can be isolated.  Ideally, the assay should be:-

•  specific, to define the  protein  of  interest  and  distinguish  it  from  all others,

• Quantitative, so that the success  of the  purification  can  be monitored, and,

• Economical in terms of time  and material.

The extent to which the assay meets these requirements has a major bearing on the difficulty,  or otherwise,  likely to  be experienced  in the subsequent protein isolation.

Assays for enzymes are usually specific although, for example, “proteolytic activity” may not be specific enough to be very useful by itself.  On the other hand,  an activity like  “toxicity”  may  not  be specific and may not  be due to  a single component.  Since a large proportion  of proteins isolated are enzymes, enzyme assays will be used to illustrate some of the  conceptual  dimensions of assays.  It  must be appreciated, however, that many proteins are not enzymes and different assay methods will be required for these.

1. Enzyme assays

Enzymes are biological catalysts which speed up the rate of specific reactions.  The activity of an enzyme is therefore  defined, and measured, by the extent to which it speeds up a reaction.

1.1 The progress curve

The primary measurement in an enzyme assay is a progress curve, in which the amount  of reaction  that  has taken  place  is plotted  against time.  The amount of reaction is defined as the amount of product formed or as the amount of substrate consumed. A typical progress curve, for an enzyme  that  is stable under the  reaction  conditions,  is shown in Fig. 1.  The velocity of the reaction is given by the slope of the progress curve. Initially, the relationship between the amount of reaction and time  is linear and the  slope of this  linear portion  gives the initial velocity (V_o). Eventually, the relationship becomes curvilinear and the  reaction  velocity  (slope  of the  line)  decreases,  eventually reaching zero when the net reaction stops. At this point, forward and reverse reactions are in equilibrium.

Figure 1. A progress curve for an enzyme-catalyzed reaction.

The progress of an enzyme  reaction  may be visualized by considering the flow of water between two tanks, one initially empty and the  other fairly full, with a pipe equipped with a tap connecting the  two tanks  at the bottom (Fig. 2).

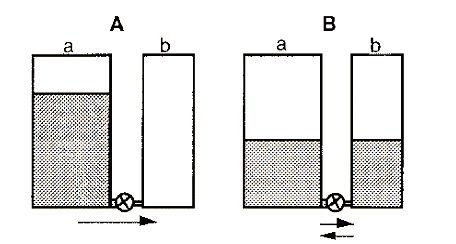
Figure 2.  The water tank analogy of an enzyme-catalyzed reaction.

In this analogy the volume of water in a tank  is analogous to  the concentration of reactant or product and the  height (potential  energy)  is analogous to its chemical potential.  Initially  (A),  there  is  a  large  amount of reactant  (a)  but no  product  (b).  The reaction will therefore flow to the right until equilibrium is reached.  The enzyme is equivalent to  the tap in this model.

1.2 The enzyme dilution curve

The initial velocity is proportional to the enzyme concentration,  a relationship expressed in an enzyme dilution curve (Fig. 3).  The  linear enzyme dilution curve forms the  basis of enzyme assays, in which the concentration of an enzyme  is estimated from a measurement of its activity (i.e. from the initial velocity of the enzyme catalyzed reaction), in the presence of an excess of substrate (to  ensure that  a substrate limitation does not restrict the initial velocity).

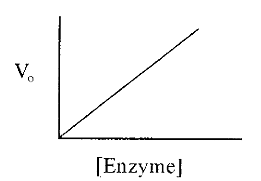
Figure 3. An enzyme dilution curve.

1.3 The substrate dilution curve

The concentration of substrate also affects the  initial velocity,  V_o, of an enzyme-catalyzed reaction;  in the  simplest case, in a manner expressed by the so-called Michaelis-Menten equation:

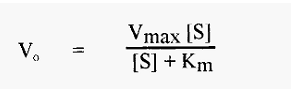
A plot of V_o versus [S] yields a so-called substrate dilution curve,  such as shown in Fig. 4, which was calculated  from  the  Michaelis-Menten equation, using values of V_max = 1000 and K_m = 90.

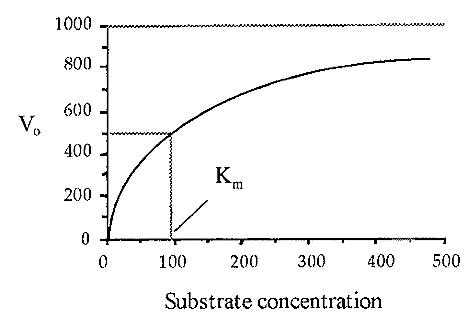
Figure 4. A substrate dilution curve.

Note: The substrate dilution curve must  not be confused with the similarly-shaped progress curve. The K_m, i.e. that substrate concentration which gives one half of the maximal velocity possible (at that  enzyme  concentration)  is a constant. characteristic for a particular enzyme acting on a particular substrate. Knowledge of the  K_m is useful when devising an enzyme  assay as it enables one to  use a substrate  concentration  where  V_o will not  be too sensitive to small changes in [S] due to experimental  error.  A good rule-of-thumb is that  [S] should be as high as possible, preferably at a level where the substrate dilution curve is asymptotic to V_max. Often, however, [S] is constrained by cost  or experimental  practicability,  and values of less than Km may have to be used.  For example the  proteinase  cathepsin B is routinely assayed at [S] = 1/4 K_m, using a fluorogenic substrate.

1.4 The effect of pH on enzyme activity

Another factor which influences V_o is pH, which can exert its effect in different ways; on the ionization of groups in the enzyme's active site, on the ionization of groups in the  substrate, or by affecting the conformation of the either the enzyme or the substrate,  These effects are manifest in changes in the kinetic constants, K_m and k_cat.

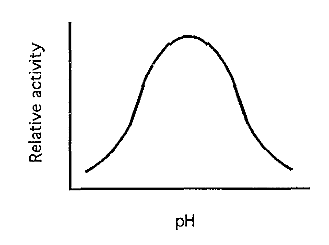
Figure 5.  A typical pH-activity curve.

The net result is usually a bell-shaped pH-activity profile (Fig.  5).  V_o  reaches its maximum at the optimum pH, which is the  pH that  should be used when  assaying the  enzyme.

In expressing pH-activity profiles, many  authors  plot  k_cat/K_m against pH. Why, and what does this mean?. For a reaction of the form:-

the initial velocity, expressed as a function of the concentrations of free enzyme [E] and substrate, is described by the equation:-

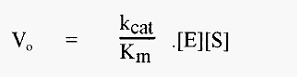
in which k_cat/K_m is readily recognized as a second order rate  constant. k_cat/K_m is also known as the specificity constant as it is maximal  with an optimum substrate.

Changes in pH will affect V_o, linearly,  through  effects  on  either  (or both of)  the  enzyme's  affinity  for  the  substrate (K_m) or  its turnover number (k_cat), but will not  affect  [E]  or  [S]. The influence of pH is, therefore, essentially on k_cat/K_m and _kcat/K_m is maximal at the  pH optimum.

The practical problem  is that [E], the concentration of free enzyme, is not  known.  In  the  measurements  involved  in establishing  a  pH-activity profile, the total enzyme concentration,  [E]_o, and the  initial substrate concentration,  [S]_o, are constant  (and known),  and in the measurement of V_o it can be assumed that  [S]  [S]_o. The concentration of free enzyme.  [E],  is not  known  but is a function  of [S] and Km asdescribed by equation 3:-

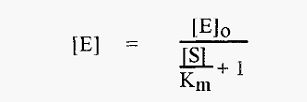
[E] is thus markedly influenced by the magnitude of [S] relative to K_m. The variation of [E] with Km is least when [S] is small relative to  K_m (Modeling of equation 3 reveals that [S] must be ≤K_m/40). When this is true (and only when this is true):-

[E] ≈[E]_o,

• the  shape  of the pH-activity profile  is linearly  affected  by changes  in kcat and/or Km, brought about by the changes in pH, and

• “relative  activity”  is  proportional  to  k_cat/K_m. When these conditions apply:-

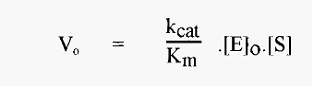
which means that,  if it is possible to  use a substrate  concentration I K_m/40, a pH-activity profile of k_cat/K_m versus pH can  be  constructed from measurements of Vo at different pH values and the  known  values of  [E]o and [S].

However, it is not always practicable to  use a substrate concentration of I  K_m/40 and when [S] is  not small relative to  K_m, [E]≠  [E]o and the more familiar Michaelis-Menten equation applies, i.e.

In this  case separate  measures of k_cat and K_m have to be obtained in the classical way by measuring V_o at a number of levels of [S], at each pH.

The paired data can be used to obtain estimates of k_cat and K_m at each pH, preferably by the  method  of Eisenthal  and Cornish-Bowden. From these, k_cat/K_m values can be obtained and the pH-activity profile plotted.

1.5 The effect of temperature on enzyme activity

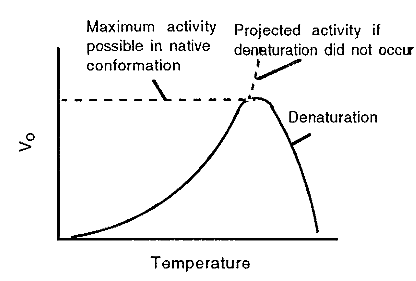
Figure 6. A typical temperature profile for an enzyme-catalyzed reaction.

Finally, temperature also influences V_o. Two effects interact to give a resultant curve.  On the one  hand, like all chemical  reactions,  the velocity of enzyme-catalyzed reactions increases with an increase in temperature, typically doubling for every 10C rise in  temperature.  In the case of an enzyme-catalyzed reaction,  however,  eventually  a temperature is reached where the enzyme becomes unstable and begins to denature, at which point the reaction rate again declines.  The resultant is usually an asymmetrical  peak,  which  rises  relatively  slowly  with  an increase in temperature, and then drops rather suddenly (Fig.  6).

It must be realized that  denaturation  is itself a reaction,  with a temperature-dependent rate constant.  Denaturation is generally a first-order reaction,  since each protein molecule simply unfolds,  independently of interaction with any other protein molecules. A useful way of expressing the temperature stability of an enzyme is therefore to measure the half-life (t_1/2) of its activity as a function of temperature.  The  half -life  is the time taken for the enzyme activity to decrease from any value to  half  of that  value.  The  half-life will  be  “infinite”  until  the temperature is reached at which the enzyme begins to denature. Thereafter, the half-life will decrease with an increase in temperature.

References

-Dennison, C. (2002). A guide to protein isolation . School of Molecular mid Cellular Biosciences, University of Natal . Kluwer Academic Publishers new york, Boston, Dordrecht, London, Moscow .

-Eisenthal, R. and Cornish-Bowden, A.  (1974) The direct linear plot. A new graphical procedure for estimating enzyme kinetic parameters. Biochem. J.  139, 715-720.