
LINEWIDTH
 المؤلف:
Mark Csele
المؤلف:
Mark Csele
 المصدر:
FUNDAMENTALS OF LIGHT SOURCES AND LASERS
المصدر:
FUNDAMENTALS OF LIGHT SOURCES AND LASERS
 الجزء والصفحة:
p101
الجزء والصفحة:
p101
 10-3-2016
10-3-2016
 2339
2339
LINEWIDTH
We often think of a laser transition as a single, sharp, well-defined wavelength. Indeed, compared to the emission characteristics of an incoherent source, it is, but under closer examination we see that a laser line does indeed have a finite bandwidth. The primary reason to broaden a line’s spectral width (the range of wavelengths it covers) is the Doppler effect, commonly associated with train whistles. Gas molecules in a laser tube are often hot and travel at high speeds. Assuming that the average speed of a gas molecule is v and that gas molecules can move in either direction at this speed, the spread in frequencies seen in the output of the laser will be
 (1.1)
(1.1)
where v is the output frequency of the laser, v0 the center frequency (=λ0/c), and v the average velocity of gas molecules. This situation is outlined in Figure 1.1, where a gas molecule is seen emitting radiation. If the molecule moves toward the observer when emitting radiation, the frequency of the radiation appears to increase (as does the sound of an approaching train blowing a whistle, in which case the frequency of the whistle is heard to increase in pitch as the train approaches). Similarly, the frequency
decreases if the molecule speeds away from the observer when emitting a photon of light (in this case, v2 in the figure). This will yield two values for the frequency of the laser, one minimum and one maximum, which will define the range of outputs of the laser. The easy way to calculate gas molecule velocity is to use kinematics and equate kinetic energy to thermal energy as follows:
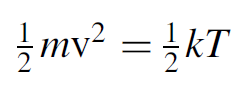 (1.2)
(1.2)
where m is the mass of the molecule, v the velocity of gas molecules (unknown), k is Boltzmann’s constant, and T is the temperature in kelvin.
The range of frequencies possible is now found by computing v given molecular mass and temperature, then substituting into the equation above to find the minimum

Figure 1.1. Doppler effect on gas molecules.
and maximum frequencies. Although this will yield a reasonable answer, we know from kinematics that the velocities of gas molecules follow a Maxwell distribution. Using such a distribution will give a more precise answer. In this manner we may compute the full width half maximum (FWHM) of the resulting output. This will yield the width (in hertz) of the optical gain profile
 (1.3)
(1.3)
where Δv is the FWHM of the output (in hertz), v0 the center frequency (at maximum gain), k is Boltzmann’s constant, T is the temperature of the gas in kelvin, M the atomic mass of the atom or molecule, and c the speed of light.
Example 1.1 Linewidth of a He Ne Laser Consider the linewidth of a He Ne laser. The laser has a gas temperature (in the actual plasma tube itself) of 1508C and an output wavelength of 632.8 nm in the red. In this laser the active lasing atom is neon (helium is present only as an energy-level pump). Neon has an atomic number of 10 and so has an atomic mass of 20.
SOLUTION First, calculate the mass of the atom as

This is then substituted into the Maxwell distribution formula:

This corresponds to a wavelength FWHM of 0.002 nm. Indeed, this is small compared to the FWHM of any incoherent light source but is still a far cry from a “single line.”
You will note that linewidth is a function of temperature, as depicted in Figure 1.2. Gas lasers that operate at high temperatures, such as the argon-ion laser, have larger line widths than that of the helium–neon laser, which operates at a relatively low temperature. Despite the fact that the graph shows temperatures up to 6000 K, He Ne lasers would normally never exceed 450 K. In the case of the argon laser, though, high temperatures are unavoidable: Discharge currents of 10

Figure 1.2. Linewidth versus temperature for a He Ne laser.

Figure 1.3. Gain curve for a practical laser.
to 70 A are common in such a laser. The resulting plasma temperatures can reach 5000 K! Techniques exist to reduce line widths.
The Doppler broadening mechanism depicted in Figure 1.1 applies not only to gas lasers where gas molecules may move freely in a tube, but also to solid-state lasers. Although atoms in a solid-state laser crystal will not move as gas molecules do, the lattice of a solid-state laser crystal will vibrate more with increasing temperature. This vibration will affect the system by making the energy band broader, and hence increase the spectral linewidth. The results of broadening are that the gain is not maximum at a specific wavelength and zero at all other wavelengths but rather, is a curve with maximum gain that gradually tapers off to zero at wavelengths around the maximum, as illustrated in Figure 1.3.
At all points on the gain curve where the gain is sufficient to overcome losses in the laser (and the laser cavity is resonant), the laser may oscillate and have output. There is a further complication in this scenario: the cavity itself, which acts as an interferometer resonant only at certain wavelengths. The configuration of the cavity leads to longitudinal modes: a series of discrete frequencies close together. Collectively, these resemble a broad line much wider, spectrally, than a single line.
 الاكثر قراءة في مواضيع عامة في الليزر
الاكثر قراءة في مواضيع عامة في الليزر
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


