
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
LIGHT EMITTING DIODES
المؤلف:
Mark Csele
المصدر:
FUNDAMENTALS OF LIGHT SOURCES AND LASERS
الجزء والصفحة:
p44
8-3-2016
3591
LIGHT EMITTING DIODES
In its simplest form, an LED is simply a diode (or p-n junction) in which flowing current generates electron hole pairs that recombine and emit excess energy in the form of a photon of light. As current flow through the diode is increased, so is the rate of electron–hole pair production and hence the rate of recombination of charge carriers (since they must flow through the device). As such, the output intensity of an LED is expected to be proportional to current flowing through the device. Consider now a practical device in which radiative and non-radiative processes are competing. Radiative processes, of course, result in production of a photon in order to recombine electrons and holes, but non-radiative processes still occur in all semiconductors. A given semiconductor material is characterized by two lifetimes, a radiative lifetime and a non-radiative lifetime corresponding to each process. If the radiative lifetime is longer than the non-radiative lifetime (as it is in silicon and other indirect-gap semiconductors), electrons and holes recombine by non-radiative processes long before radiative emissions occur, so no light is produced. This is why silicon diodes do not emit light when conducting (if they did, it would be in the infrared, due to the small band gap). If, on the other hand, the radiative lifetime is shorter, light is emitted as the primary end product of recombination of electrons and holes. Gallium arsenide and other direct-gap semiconductors have this favorable situation and so are good choices for light emitters. Assuming that photons are emitted, their energy should, ideally, be equal to the band gap energy Eg. The problem here is that electrons in each energy band are not at a single discrete value of energy (in our simplistic model above, we assumed these levels to be the bottom of the conduction band and the top of the valence band) but rather, may have a variety of energy values anywhere inside the bands. We may predict the most probable value as well as the distribution of electrons in a band using a Fermi Dirac distribution function which describes the probability of occupancy of an energy state. There are a wide variety of possible structures for LEDs, but for simplicity let’s consider a common red LED. Statistics show that the maximum population of electrons in the conduction band will occur at ½ kT above the bottom of the band (where k is Boltzmann’s constant and T is the temperature in kelvin), where the energy of the bottom of the conduction band is defined by a voltage Ec. Similarly, the maximum population of holes in the valence band will be found ½ kT below the top of the band, defined by a voltage Ev. The concentration of charge carriers (both holes and electrons) per unit energy is plotted in Figure 1.1. In this situation we expect, then, to find maximum spectral output at a wavelength corresponding to Eg + kT, the point where the concentration is maximum, not at Eg as thought originally. There will also be a spread in photon energies, since there are many possible energies in recombination, also depicted in Figure 1.1. The lowest-energy photons at λr will be shifted toward the red since these have the least energy. The maximum output of the device is expected at λp, where the maximum concentration lies. Photons will then be emitted into the “violet-shifted” side of the peak, as the concentrations of charge carriers taper off slowly throughout the band. The width of each band (both electrons and holes as shown in the figure) is approximately 2kT at the halfway point, so a considerable spread in energies is possible (and the spread becomes wider as the device is elevated in temperature). Using the model described above, built solely on the thermal distribution of electrons in each band, we can predict the emission spectra of LEDs numerically. A typical red LED with a measured band gap voltage of 1.95 V should have a
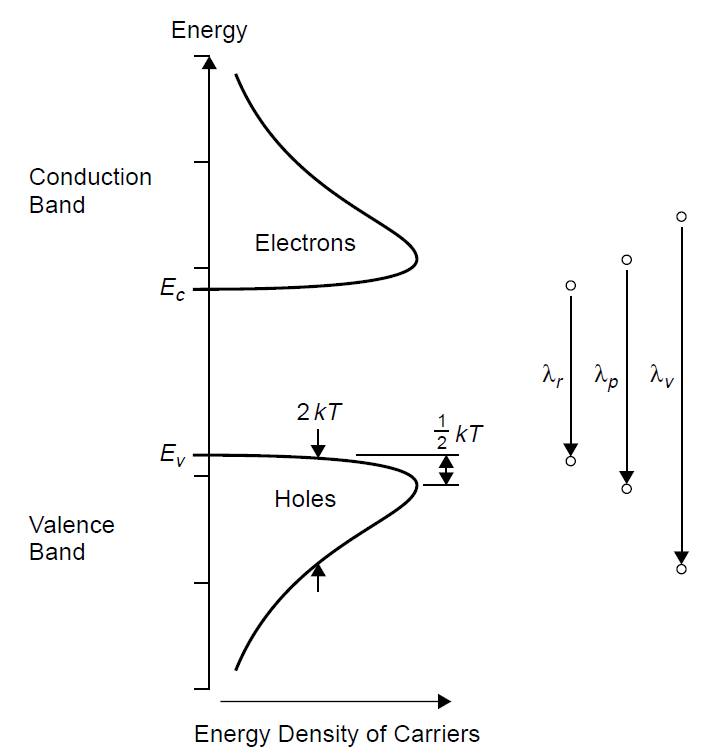
Figure 1.1. Energy distributions and possible photon energies.
peak emission of photons with energy equal to
Epeak emission = hv + kT (1.1)
where k is Boltzmann’s constant and T is the temperature. Substituting for hv = 1.95 eV and assuming a temperature of 300 K, the peak emission is expected at 628 nm. Further, we expect a spread of photon energies equal to about 4kT since each band has a width of 2kT. The minimum photon energy will be the band gap at 1.95 eV (corresponding to 636 nm) and the maximum photon energy will be 1.95 eV+ 4kT (corresponding to 604 nm). The FWHM expected is then 32 nm. In addition to the numerical predictions for the spectrum, we expect that the shape of the output spectrum will feature a sharp cutoff at the red (long-wavelength) side of the spectrum, since the minimum photon energy possible is well defined (where a jump between Ec and Ev is the smallest possible energy). This theoretical prediction as well as the output of an actual red LED is plotted in Figure 1.2 for comparison. It is evident that the predictions of the output spectrum of the LED, based on energy distributions, are wrong. The spectrum of the actual LED is, as predicted by the model, asymmetrical; however, if you examine each plot carefully you will note that the model predicts a long violet tail on the spectrum and a rather abrupt cutoff on the red side of the emission spectrum. An actual red LED exhibits the opposite behavior! To account for the actual spectrum

Figure 1.2. Predicted and actual output spectrum of a red LED.
of a real device we must factor into the model absorption of emitted light by the material itself (an important concept and one that will be seen again when discussing fast-pulsed lasers such as the nitrogen laser) as well as the effect of energy levels of the impurities added to manufacture p- and n-type semiconductors from which this device is made. Absorption of light by the semiconductor material itself occurs when photons have an energy at or exceeding the band gap. For photons with lower energies than the band gap (i.e., those on the red side of the spectrum), absorption should not occur, since photons lack the energy to excite electrons from the valence band to the conduction band and hence are not absorbed. The effect is seen as a sharper cutoff on the violet side of the spectrum than predicted by the model, as evident in Figure 1.2. The effect of impurity energy levels is most obvious when considering the lack of the sharp red cutoff predicted by the model. Transitions with less energy than the band gap must originate or terminate at energy levels within the gap itself; however, this is logically impossible since this is a forbidden region where no energy levels exist at least energy levels from the semiconductor itself. The problem with any semiconductor is that impurities such as phosphorus, aluminum, and boron are added to the base semiconductor material to make p- and n-type material for the junction. These atoms have their own energy levels (or should we say bands, since they, too, are in the crystal lattice?). Many of these levels exist at energies within the forbidden region (i.e., the band gap for the semiconductor), so transitions are possible from and to these intermediate levels. In many cases the energy bands from the impurities are at energies just below the conduction band or just above the valence band. The effect is that photon emission is possible at energies lower than the band gap energy, so the tail on the red side of the spectrum extends into energies that are not possible for the semiconductor material. Of course, this also serves to broaden the spectral width of the emission practical LEDs typically have a FWHM of 25 to 40 nm. It is possible to design the structure and dopant levels of LEDs to minimize absorption and hence increase efficiency. Efficiencies of up to 30% have been achieved with such optimizations, making the LED about three times as efficient a light source as a tungsten filament lamp.
 الاكثر قراءة في الضوء
الاكثر قراءة في الضوء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















